
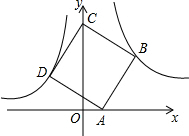
 如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{4}{x}$(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点D在双曲线y=-$\frac{4}{x}$(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形分析 (1)把B的坐标代入求出即可;
(2)设MD=a,OM=b,求出ab=4,过D作DM⊥x轴于M,过B作BN⊥x轴于N,证△ADM≌△BAN,推出BN=AM=3,MD=AN=a,求出a=b,求出a的值即可.
解答 解:(1)∵点B(3,3)在双曲线y=$\frac{k}{x}$上,
∴k=3×3=9;
(2)∵B(3,3),
∴BN=ON=3,
设MD=a,OM=b,
∵D在双曲线y=-$\frac{4}{x}$(x<0)上,
∴ab=4,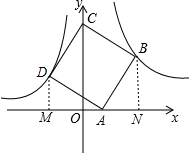
过D作DM⊥x轴于M,过B作BN⊥x轴于N,
则∠DMA=∠ANB=90°,
∵四边形ABCD是正方形,
∴∠DAB=90°,AD=AB,
∴∠MDA+∠DAM=90°,∠DAM+∠BAN=90°,
∴∠ADM=∠BAN,
在△ADM和△BAN中,
$\left\{\begin{array}{l}{∠MDA=∠NAB}\\{∠DMA=∠ANB}\\{AD=BA}\end{array}\right.$,
∴△ADM≌△BAN(AAS),
∴BN=AM=3,DM=AN=a,
∴0A=3-a,
即AM=b+3-a=3,
a=b,
∵ab=4,
∴a=b=2,
∴OA=3-2=1,
即点A的坐标是(1,0).
点评 本题考查了正方形的性质,反比例函数图象上点的坐标特征,全等三角形的性质和判定的应用,主要考查学生运用性质进行推理和计算的能力.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | -2和-0.5 | B. | -2和-1 | C. | -2和-1.5 | D. | -2和-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
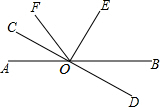 如图,直线AB和CD相交于O点,OC⊥OE,OC平分∠AOF,∠EOF=56°,
如图,直线AB和CD相交于O点,OC⊥OE,OC平分∠AOF,∠EOF=56°,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1<x3<x2 | B. | x<1x2<x3 | C. | x3<x2<x1 | D. | x2<x3<x1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球次数 | 10 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 出现红球的频数 | 4 | 9 | 16 | 31 | 44 | 61 | 74 | 92 | 118 | 147 |
| 出现白球的频数 | 5 | 7 | 18 | 33 | 54 | 78 | 101 | 123 | 159 | 202 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{20}$ | D. | $\sqrt{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线互相垂直平分的四边形是正方形 | |
| D. | 两组对角分别相等的四边形是平行四边形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com