

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源:不详 题型:填空题
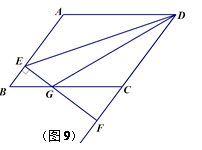
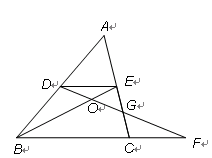
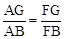 ;②点F是GE的中点;③AF=
;②点F是GE的中点;③AF=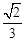 AB;④S△ABC=5S△BDF,其中正确的结论序号是 ▲ .
AB;④S△ABC=5S△BDF,其中正确的结论序号是 ▲ .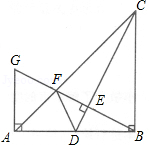
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
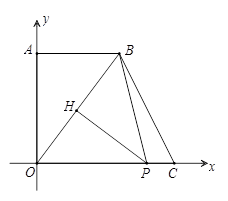
 中,
中,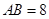 ,
,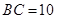 ,
,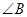 为锐角,
为锐角,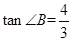 .
. 为线段
为线段 上的一个动点(不包括端点),
上的一个动点(不包括端点),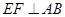 ,交射线
,交射线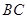 于点
于点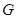 ,交射线
,交射线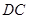 于点
于点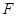 .
.
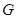 在线段
在线段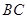 上,求
上,求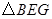 与
与 的周长之和
的周长之和 的运动过程中,
的运动过程中,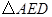 与
与 是否会相似?如果相似,请求出
是否会相似?如果相似,请求出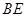 的长;如果不相似,请说明理由.
的长;如果不相似,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
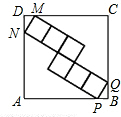
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com