

| EF2-CE2 |
| 3 |
| AB |
| FC |
| BF |
| EC |
| 3x | ||
|
| BF |
| x |
| 3 |
| EF2-CE2 |
| 2 |
| AB |
| FC |
| BF |
| EC |
| 4x | ||
2
|
| BF |
| x |
| 2 |
| EF2-CE2 |
| 15 |
| AB |
| FC |
| BF |
| EC |
| 5x | ||
|
| BF |
| x |
| ||
| 3 |
| EF2-CE2 |
| n2-1 |
| AB |
| FC |
| BF |
| EC |
| (n+1)x | ||
|
| BF |
| x |
| ||
| n-1 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:044
某名牌白酒最近六年的价格变化如下表所示:
甲、乙两名销售员根据上述数据分别绘制了折线统计图,如图所示,


(1)上述两个图中,哪个更令人觉得该酒的价格上涨的速度快?
(2)仔细比较这两个图,它们所表示的数据相同吗?
(3)为什么两个图给人不同的感觉?
查看答案和解析>>
科目:初中数学 来源:2014届江苏苏州市初二第二学期期末考试数学试卷(解析版) 题型:解答题
如下4个图中,不同的矩形ABCD,若把D点沿AE对折,使D点与BC上的F点重合;
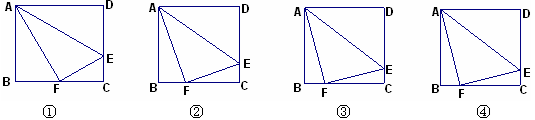
(1)图①中,若DE︰EC=2︰1,求证:△ABF∽△AFE∽△FCE;并计算BF︰FC;
(2)图②中若DE︰EC=3︰1,计算BF︰FC= ;图③中若DE︰EC=4︰1,计算BF︰FC= ;
(3)图④中若DE︰EC= ︰1,猜想BF︰FC= ;并证明你的结论
︰1,猜想BF︰FC= ;并证明你的结论
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com