
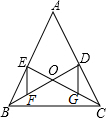
 如图,△ABC的中线BD,CE相交于点O,点F,G分别是OB,OC的中点,则有EF∥DG,EF=DG,试说明理由.
如图,△ABC的中线BD,CE相交于点O,点F,G分别是OB,OC的中点,则有EF∥DG,EF=DG,试说明理由. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
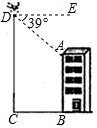 如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,求教学楼的高度AB.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】
如图,某校无人机兴趣小组借助无人机测量教学楼的高度AB,无人机在离教学楼底部B处16米的C处垂直上升31米至D处,测得教学楼顶A处的俯角为39°,求教学楼的高度AB.(结果精确到0.1米)【参考数据:sin39°=0.63,cos39°=0.78,tan39°=0.81】查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)我们知道,将一条线段AB分割成大小两条线段AP、PB,使AP>PB,点P把线段AB分成两条线段AP和BP,且$\frac{AP}{AB}$=$\frac{BP}{AP}$,点P就是线段AB的黄金分割点,此时$\frac{PA}{AB}$的值为$\frac{\sqrt{5}-1}{2}$ (填一个实数):
(1)我们知道,将一条线段AB分割成大小两条线段AP、PB,使AP>PB,点P把线段AB分成两条线段AP和BP,且$\frac{AP}{AB}$=$\frac{BP}{AP}$,点P就是线段AB的黄金分割点,此时$\frac{PA}{AB}$的值为$\frac{\sqrt{5}-1}{2}$ (填一个实数):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
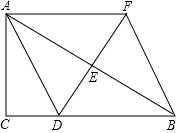 如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,联结BF.
如图,在△ABC中,∠C=90°,点D为边BC上一点,点E为边AB的中点,过点A作AF∥BC,交DE的延长线于点F,联结BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com