
分析 先化简题目中的式子,然后根据a2-3a+2=0可得a的值,注意a的值要使得原分式有意义,本题得以解决.
解答 解:(a-$\frac{2a}{a+1}$)÷($\frac{{{a^2}-2a+1}}{{{a^2}-1}}$)
=$\frac{a(a+1)-2a}{a+1}×\frac{(a+1)(a-1)}{(a-1)^{2}}$
=$\frac{{a}^{2}-a}{a-1}$
=$\frac{a(a-1)}{a-1}$
=a,
由a2-3a+2=0,得a=1或a=2,
∵当a=1时,a-1=0,使得原分式无意义,
∴a=2,原式=2.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


科目:初中数学 来源: 题型:选择题
| A. | 投掷一枚均匀的硬币,正面朝上的概率是$\frac{1}{2}$ | |
| B. | 投掷一枚图钉,钉尖朝上、朝下的概率一样 | |
| C. | 投掷一枚均匀的骰子,每一种点数出现的概率都是$\frac{1}{6}$,所以每投6次,一定会出现一次“l点” | |
| D. | 投掷一枚均匀的骰子前默念几次“出现6点”,投掷结果“出现6点”的可能性就会加大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{5}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
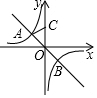 如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )
如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O的半径为3,PA、PB分别切⊙O于点A、B,OP=6,则PB的长为( )
如图,⊙O的半径为3,PA、PB分别切⊙O于点A、B,OP=6,则PB的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>2 | B. | x>4 | C. | 2<x<4 | D. | 无解 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com