
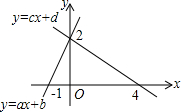 如图所示,可以得出不等式组
如图所示,可以得出不等式组
|
科目:初中数学 来源: 题型:
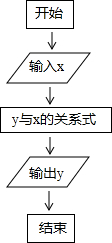 按如图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
按如图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版) 题型:解答题
 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;
查看答案和解析>>
科目:初中数学 来源:2011-2012学年安徽省合肥市琥珀中学九年级(上)第一次段考数学试卷 (解析版) 题型:解答题
 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;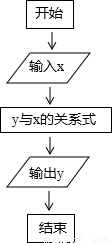
查看答案和解析>>
科目:初中数学 来源:第23章《二次函数与反比例函数》中考题集(40):23.5 二次函数的应用(解析版) 题型:解答题
 时,这种变换满足上述两个要求;
时,这种变换满足上述两个要求;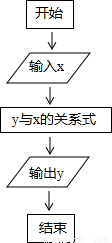
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com