分析:(1)根据平方法解无理方程,然后验证即可得出答案;
(2)先化简后解一元二次方程即可得出答案;
(3)先取分母,根据增根代入求出a的值即可;
(4)先取分母,再求a的范围,根据增根验证a不能取的值即可;
(5)两边同乘以(x
2-1),化简检验后即可得出答案;
(6)将原方程整理配方得
(-1)2+(-1)2+(-1)2=0,根据非负数的和为0各个数都是0即可求解;
解答:解:(1)两边平方得:x+2=x
2,
解得:x=-1或x=2,
∵-x≥0,
∴x=-1;
(2)由已知得
-=,
即
-=,
方程两边同时乘以4(a+1),(a+1),得
36(a-1)-4(a+1)=7(a+1)(a-1)
化简得7a
2-32a+33=0,于是
a1=,a2=3;
(3)将原方程去分母得3(x+1)+(ax+3)x=2(x+1)x,
因为原方程有增根x=-1,所以代入上面方程得
3(-1+1)+(-a+3)•(-1)=2(-1+1)•(-1),
即a-3=0,求得a=3;
(4)原方程去分母得
x=,∵
x>0即
>0,
故a<2,
再令x=2,则
=2,
∴a=-4,
由于x=2为原方程的增根,
∴a≠4,于是有a<2且a≠-4.
(5)①
1-=两边同乘以(x
2-1),得(x
2-1)-(x-1)=2,
化简得x
2-x-2=0,
即x
1=2,x
2=-1.
经检验得x
1=2是原方程根,x=-1是增根.
∴原方程的根是x=2;
②移项得:
=1-3x,
两边平方得:6x(x-1)=0,
∴x=0或x=1,
当x=1时,代入不符合题意,故x=0;
(6)将原方程整理配方得
(-1)2+(-1)2+(-1)2=0∴
-1=-1=-1=0,
解之得
.
点评:本题考查了解无理方程和解分式方程,属于基础题,关键是注意增根的验证即可.



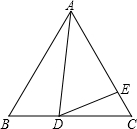 已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-