

分析 (1)设ON的反向延长线为OD,由旋转的性质可知∠M=30°,∠MNO=60°,从而可分别求得∠BON=∠AOD=∠COD=30°;
(2)分别用∠AON表示出∠AOM和∠NOC即可.
解答 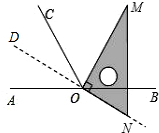 解:
解:
(1)直线ON平分∠AOC.
理由如下:
如图,设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB=$\frac{1}{2}∠BOC=\frac{1}{2}×{120°}={60°}$,
又∠MOD=∠MON=90°,
∴∠COD=90°-∠BOC=30°,
∵∠AOC=180°-∠BOC=60°,
∴∠COD=$\frac{1}{2}$∠AOC,
∴OD平分∠AOC,
即直线ON平分∠AOC;
(2)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°-∠AON,∠NOC=60°-∠AON,
∴∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.
点评 本题主要考查旋转的性质及直角三角形的性质,掌握旋转的性质是解题的关键,即旋转前后对应的线段和角分别相等.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
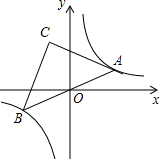 如图,点A是双曲线y=$\frac{4}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
如图,点A是双曲线y=$\frac{4}{x}$在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )| A. | y=-$\frac{1}{4}$x | B. | y=-$\frac{1}{2}$x | C. | y=-$\frac{4}{x}$ | D. | y=-$\frac{2}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.
如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3<x<0 | B. | x<0 | C. | -3<x<2 | D. | x>-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把△ABC沿AB平移到△A′B′C′的位置,它们的重叠部分的面积是△ABC面积的一半,若AB=$\sqrt{2}$,求此三角形移动的距离A′A.
如图,把△ABC沿AB平移到△A′B′C′的位置,它们的重叠部分的面积是△ABC面积的一半,若AB=$\sqrt{2}$,求此三角形移动的距离A′A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图A(-4,0),C(0,3),将线段CA以点C为旋转中心旋转,所得的对应线段记为CA',当点A'落在y轴上时,写出A'的坐标,并求出以A'为顶点,经过A(-4,0)的抛物线的解析式.
如图A(-4,0),C(0,3),将线段CA以点C为旋转中心旋转,所得的对应线段记为CA',当点A'落在y轴上时,写出A'的坐标,并求出以A'为顶点,经过A(-4,0)的抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的顶点C,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点A,B分别在x轴和y轴的正半轴上,再在其右侧作正方形EFDG,顶点G在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点E在x轴的正半轴上,则点G的坐标为(2$\sqrt{3}$+2,2$\sqrt{3}$-2).
如图,正方形ABCD的顶点C,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点A,B分别在x轴和y轴的正半轴上,再在其右侧作正方形EFDG,顶点G在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点E在x轴的正半轴上,则点G的坐标为(2$\sqrt{3}$+2,2$\sqrt{3}$-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com