
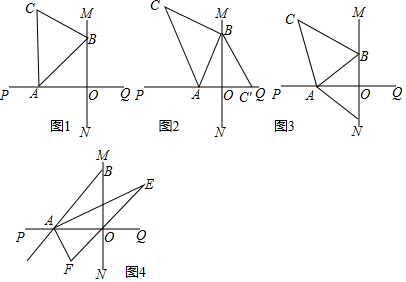
分析 (1)由直线MN与直线PQ垂直相交于O,得到∠AOB=90°,根据三角形的外角的性质得到∠PAB+∠ABM=270°,根据角平分线的定义得到∠BAC=$\frac{1}{2}$∠PAB,∠ABC=$\frac{1}{2}$∠ABM,于是得到结论;
(2)由于将△ABC沿直线AB折叠,若点C落在直线PQ上,得到∠CAB=∠BAQ,由角平分线的定义得到∠PAC=∠CAB,根据三角形的内角和即可得到结论;根据将△ABC沿直线AB折叠,若点C落在直线MN上,得到∠ABC=∠ABN,由于BC平分∠ABM,得到∠ABC=∠MBC,于是得到结论;
(3)由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=$\frac{1}{2}$∠BAO,∠EOQ=$\frac{1}{2}$∠BOQ,进而得出∠E的度数,由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°,在△AEF中,由一个角是另一个角的$\frac{3}{2}$倍分两种情况进行分类讨论.
解答 解:(1)∠ACB的大小不变,
∵直线MN与直线PQ垂直相交于O,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°,
∴∠PAB+∠ABM=270°,
∵AC、BC分别是∠BAP和∠ABM角的平分线,
∴∠BAC=$\frac{1}{2}$∠PAB,∠ABC=$\frac{1}{2}$∠ABM,
∴∠BAC+∠ABC=$\frac{1}{2}$(∠PAB+∠ABM)=135°,
∴∠ACB=45°;
(2)∵将△ABC沿直线AB折叠,若点C落在直线PQ上,
∴∠CAB=∠BAQ,
∵AC平分∠PAB,
∴∠PAC=∠CAB,
∴∠PAC=∠CAB=∠BAO=60°,
∵∠AOB=90°,
∴∠ABO=30°,
∵将△ABC沿直线AB折叠,若点C落在直线MN上,
∴∠ABC=∠ABN,
∵BC平分∠ABM,
∴∠ABC=∠MBC,
∴∠MBC=∠ABC=∠ABN,
∴∠ABO=60°,
故答案为:30°,60°;
(3)∵∠BAO与∠BOQ的角平分线相交于E,
∴∠EAO=$\frac{1}{2}$∠BAO,∠EOQ=$\frac{1}{2}$∠BOQ,
∴∠E=∠EOQ-∠EAO=$\frac{1}{2}$(∠BOQ-∠BAO)=$\frac{1}{2}$∠ABO,
∵AE、AF分别是∠BAO和∠OAG的角平分线,
∴∠EAF=90°.
在△AEF中,
∵有一个角是另一个角的$\frac{3}{2}$倍,故有:
①∠EAF=$\frac{3}{2}$∠F,∠E=30°,∠ABO=60°;
②∠F=$\frac{3}{2}$∠E,∠E=36°,∠ABO=72°;
∴∠ABO为60°或72°.
点评 本题考查了翻折变换-折叠问题,三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
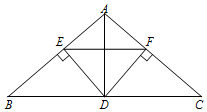 如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E、F,△AEF∽△ABC.
如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E、F,△AEF∽△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一个三角形的算法图,每个方框里有一个数,这个数等于它所在边的两个圆圈里的数的和,则图中①②③三个圆圈里的数依次是( )
如图是一个三角形的算法图,每个方框里有一个数,这个数等于它所在边的两个圆圈里的数的和,则图中①②③三个圆圈里的数依次是( )| A. | 19,7,14 | B. | 11,20,19 | C. | 14,7,19 | D. | 7,14,19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
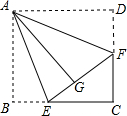 如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
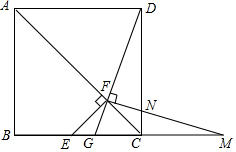 如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.
如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com