
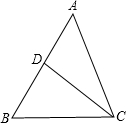
 已知,D是△ABC的AB边上的一点,BD=
已知,D是△ABC的AB边上的一点,BD= ,AB=3,BC=2
,AB=3,BC=2 ,AB=3,BC=2,
,AB=3,BC=2, =
= ,
, =
= ,
, =
= ,
,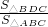 =(
=( )2=
)2= ,
, ,AB=3,BC=2,得到
,AB=3,BC=2,得到 =
= ,
, =
= ,即
,即 =
= ,加上∠B公共,得到△BCD∽△CBA;
,加上∠B公共,得到△BCD∽△CBA;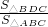 =(
=( )2=
)2= ,而△BCD的面积是4,得到S△ADC的值.
,而△BCD的面积是4,得到S△ADC的值.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
 (2012•厦门)已知:⊙O是△ABC的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC.
(2012•厦门)已知:⊙O是△ABC的外接圆,AB为⊙O的直径,弦CD交AB于E,∠BCD=∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点O是△ABC的∠ABC和∠ACB平分线的交点,过O作EF平行于BC交AB于E,交AC于F,AB=12,AC=18,则△AEF的周长是( )
如图,已知点O是△ABC的∠ABC和∠ACB平分线的交点,过O作EF平行于BC交AB于E,交AC于F,AB=12,AC=18,则△AEF的周长是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com