
��֪��������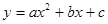 ��a��0���Ķ���M������Ϊ��1,��2����y�ύ�ڵ�C��0��
��a��0���Ķ���M������Ϊ��1,��2����y�ύ�ڵ�C��0��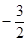 ������x�ύ��A��B���㣨A��B����ߣ�.
������x�ύ��A��B���㣨A��B����ߣ�.

��1����������ߵı���ʽ��
��2����P���߶�OB��һ���㣨�����B�غϣ�����Q���߶�BM���ƶ��ҡ�MPQ��45�㣬���߶�OP��x��MQ�� 1����y1��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
1����y1��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3�����ڣ�2�����������Ƿ���ڵ�P��ʹ��PQB��PBΪ�ĵ��������Σ������������Q�����꣬��������˵�����ɣ�
���ڣ�1���������ߵĶԳ������Ƿ���ڵ�F��ʹ��BMF�ǵ��������Σ�������ֱ��д���������������ĵ�F������.
��1��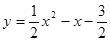 ��2��
��2��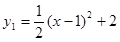 ��0��x��3����3���ٴ��ڣ�Q������Ϊ��2��1����F1��1��0����F2��1��
��0��x��3����3���ٴ��ڣ�Q������Ϊ��2��1����F1��1��0����F2��1��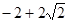 ����F3��1��
����F3��1��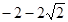 ����F4��1��2��.
����F4��1��2��.
���������⣺��1���������ߵĶ���ΪM��1����2������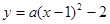 ��
��
�ɵ㣨0��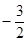 ���ã�
���ã�
 ��
��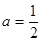 .
.
��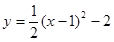 ��
��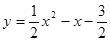 .
����������������3��
.
����������������3��
��2����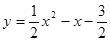 ����y��0��
����y��0��
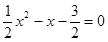
��ã�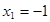 ��
��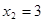
��A����1��0����B��3��0�� ����������������4��
��M��1����2��
���MBO��45�㣬MB��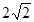
���MPQ��45��
��MBO����MPQ
�֡ߡ�M����M
���MPQ�ס�MPB ����������������5��
��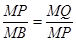
��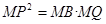
��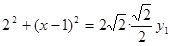
��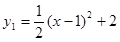 ��0��x��3��.
��0��x��3��.
��������������������7�֣��Ա���ȡֵ��Χ1�֣�
��3���ٴ��ڵ�Q��ʹQP��QB������PQB����PBΪ�ĵ��������Σ���PB�Ĵ�ֱƽ���߽�BM��Q����QP��QB.
���QPB����MBP��45��
�֡ߡ�MPQ��45�㣬
���ʱMP��x��
��P��1��0����
��PB��2.
��Q��������2��1��. ��������������������9��
��F1��1��0����F2��1��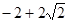 ����F3��1��
����F3��1��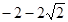 ����F4��1��2��.
����F4��1��2��.
������������������������11��
��1���������ߵı���ʽΪy=a��x-1��2-2������C��������뼴�ɵó��𰸣�
��2����֤����MPQ�ס�MPB���������Ƶ������е�ʽ����y1��x�ĺ�����ϵʽ��
��3���ټ����������������P�㣬����������PQB��PBΪ�ĵ��������Σ���PB�Ĵ�ֱƽ���߽�BM��Q��QP=QB�����P���Q�����ꣻ�ڸ��ݡ�BMF�ǵ��������Σ�ֻҪ��Fʹ�ø������ε�������ȼ��ɣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��10 | B��9 | C��8 | D��7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com