解:(1)∵抛物线y=x
2-2x+k与y轴交于点C(0,-3),
∴k=-3,
∴抛物线的解析式为y=x
2-2x-3,
令y=0,则x
2-2x-3=0,
∴(x+1)(x-3)=0,
∴x+1=0,x-3=0,
解得x
1=-1,x
2=3,
∴点A的坐标为A(-1,0),点B的坐标为B(3,0);
故答案为:-3,(-1,0),(3,0);

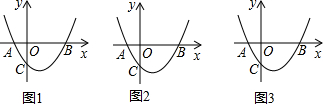
(2)如图(1),∵y=x
2-2x-3=(x-1)
2-4,
∴抛物线的顶点为M(1,-4),连接OM,
则△AOC的面积=

AO•OC=

×1×3=

,△MOC的面积=

OC•|x
M|=

×3×1=

,
△MOB的面积=

OB•|y
M|=

×3×4=6,
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=

+

+6=9;
(说明:也可过点M作抛物线的对称轴,将四边形ABMC的面积转化为求1个梯形与2个直角三角形面积的和.)
(3)如图(2),过点B作BQ
1⊥BC,交抛物线于点Q
1、交y轴于点E,连接Q
1C,
∵∠CBO=45°,

∴∠EBO=45°,BO=OE=3,
∴点E的坐标为(0,3),
∴直线BE的解析式为y=-x+3,
由
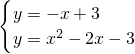
,
解得
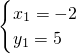
,
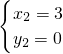
,
∴点Q
1的坐标为(-2,5);
如图(3),过点C作CF⊥CB,交抛物线于点Q
2、交x轴于点F,连接BQ
2,
∵∠CBO=45°,
∴∠CFB=45°,OF=OC=3,
∴点F的坐标为(-3,0),
∴直线CF的解析式为y=-x-3,
由
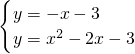
,
解得
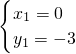
,
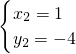
,
∴点Q
2的坐标为(1,-4).
综上,在抛物线上存在点Q
1(-2,5)、Q
2(1,-4),使△BCQ
1、△BCQ
2是以BC为直角边的直角三角形.
分析:(1)把点C的坐标代入函数解析式,然后求出k的值即可;令y=0,得到关于x的一元二次方程,解方程求出x的值,再根据点A在点B的左边,写出坐标即可;
(2)把抛物线解析式整理成顶点式,然后写出顶点坐标,再连接OM,分别求出△AOC、△MOC、△MOB的面积,然后根据四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积进行计算即可求解;
(3)因为直角顶点不明确,所以分①点B为直角顶点,设QB与y轴交于点E,根据∠CBO=45°可得∠EBO=45°,然后求出点E的坐标,再利用待定系数法列式求出直线BE的解析式,与抛物线联立求解即可;②点C为直角顶点,设CQ与x轴交于点F,根据∠CBO=45°可得∠CFB=45°,然后求出点F的坐标,再利用待定系数法列式求出直线CF的解析式,与抛物线联立求解即可.
点评:本题考查了待定系数法求二次函数解析式,三角形的面积,等腰直角三角形的性质,以及函数图象交点的求法,(3)题需要注意分直角顶点的不同进行讨论求解.


 AO•OC=
AO•OC= ×1×3=
×1×3= ,△MOC的面积=
,△MOC的面积= OC•|xM|=
OC•|xM|= ×3×1=
×3×1= ,
, OB•|yM|=
OB•|yM|= ×3×4=6,
×3×4=6, +
+ +6=9;
+6=9;
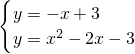 ,
,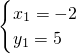 ,
,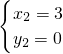 ,
,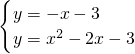 ,
,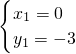 ,
,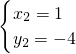 ,
,

 积为常数时,矩形ABCD需要满足什么条件并说明理由.
积为常数时,矩形ABCD需要满足什么条件并说明理由. ,且OA⊥AB,∠COB=45°.
,且OA⊥AB,∠COB=45°.

