
 ∽ △QWP;
∽ △QWP;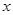 为何值时,△PQW为直角三角形?
为何值时,△PQW为直角三角形? 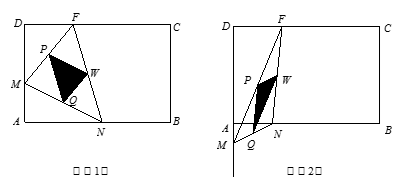
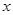 为____▲_____时,线段MN最短?
为____▲_____时,线段MN最短?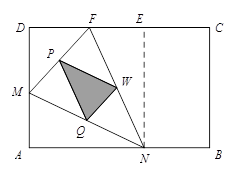
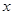
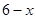 ( 2分)
( 2分)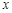 ,∴AM=4-
,∴AM=4-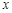 ,AN=DE=6-
,AN=DE=6-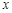
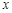
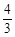 .
.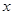 为4或
为4或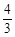 时,△PQW为直角三角形 (3分)
时,△PQW为直角三角形 (3分)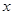 =5时,线段MN最短.(2分)解析:
=5时,线段MN最短.(2分)解析:

科目:初中数学 来源: 题型:
 根据要求完成下面的填空:如图,直线AB,CD被EF所截,若已知∠1=∠2.
根据要求完成下面的填空:如图,直线AB,CD被EF所截,若已知∠1=∠2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com