练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

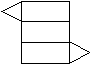
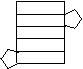
    试判断如图3中的平面图形（1）—（4）中能否折叠成一个几何体？若能，将折叠成的几何体的名称填在横线上.

     

    （4）   

     

    （3）   

     

    （1）   

    （16）   

     

    （2）   

     
     


    （1）三棱柱   （2）五棱柱    （3）正方体     （4）圆柱

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

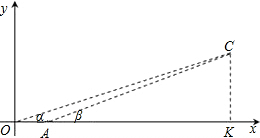
    精英家教网某特种侦察小队在一次作战行动中发现一个空中固定目标点C，并以O、A为两观察点，分别测得目标C的仰角分别是α和β，且tanα=
    9
    28
    ，tanβ=
    3
    8
    ，又OA=1千米．
    （1）建立如图所示的平面直角坐标系，根据题中提供的数据，求出目标点C的坐标；
    （2）该侦察小队及时引导武装直升机在O点正上方
    5
    3
    千米的D处向目标C发射了防空导弹，经测算，该导弹在离开D点的水平距离为4千米时，达到了最大的离地飞行高度3千米．若导弹飞行轨迹为抛物线，求其解析式；精英家教网
    （3）试判断按（2）中轨迹飞行的导弹是否能击中目标C，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．精英家教网点C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．
    （1）画出△ABC，点C的坐标是
     
    ，△ABC的面积是
     
    ；
    （2）将△ABC绕点C旋转180°得到△A1B1C，连接AB1、BA1，试判断四边形AB1A1B是何种特殊四边形，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

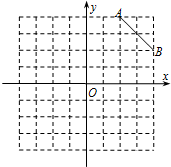
    6、在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．
    （1）填空：C点的坐标是
    （1，1）
    ，△ABC的面积是
    4
    ；
    （2）将△ABC绕点C旋转180°得到△A1B1C1，连接AB1、BA1，试判断四边形AB1A1B是何种特殊四边形，请说明理由；
    （3）请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积的2倍？若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

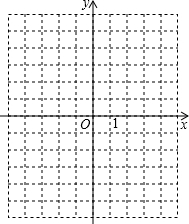    已知点A（2，2），B（-4，2），C（-2，-1），D（4，-1）．在如图所示的平面直角坐标系中描出点A、B、C、D，然后依次连结A、B、C、D得到四边形ABCD，试判断四边形ABCD的形状，并说明理由．

    查看答案和解析>>

    同步练习册答案