
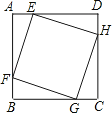
【题目】如图,已知:正方形EFGH的顶点E、F、G、H分别在正方形ABCD的边DA、AB、BC、CD上.若正方形ABCD的面积为16,AE=1,则正方形EFGH的面积为 .
【答案】10
【解析】
试题分析:根据正方形的性质找出相等的边角关系,从而证出△AFE≌△BGF≌△CHG≌△DEH,再由正方形ABCD的面积为16,AE=1,找出AF的长度,根据S正方形EFGH=S正方形ABCD﹣4S△AFE即可得出结论.
解:∵四边形ABCD、EFGH均为正方形,
∴∠A=∠B=90°,∠EFG=90°,EF=FG.
∵∠AFE+∠BFG=90°,∠BFG+∠BGF=90°,
∴∠AFE=∠BGF.
在△AFE和△BGF中, ,
,
∴△AFE≌△BGF(AAS),
∴BF=AE=1.
∵正方形ABCD的面积为16,
∴AB=4,AF=AB﹣BF=3.
同理可证出△AFE≌△BGF≌△CHG≌△DEH.
∴S正方形EFGH=S正方形ABCD﹣4S△AFE=16﹣4×![]() ×1×3=10.
×1×3=10.
故答案为:10.


科目:初中数学 来源: 题型:
【题目】△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,P为线段AB上一动点,D为BC上中点,则PC+PD的最小值为( )
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个商贩同时卖出两件上衣,售价都是135元,按成本计算,其中一件盈利25%,另一件亏损25%,在这次交易中,该商贩( )
A. 不赔不赚 B. 赚9元 C. 赔9元 D. 赔18元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.
(1)求证:EF∥AC;(2)求∠BEF大小;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com