
 如图,△ABC是一块铁皮余料.已知底边BC=160cm,高AD=120cm.在铁皮余料上截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
如图,△ABC是一块铁皮余料.已知底边BC=160cm,高AD=120cm.在铁皮余料上截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.分析 (1)先表示出AM,再根据相似三角形对应高的比等于相似比列式整理即可;
(2)根据矩形的面积公式列式整理,再根据二次函数的最值问题求解即可.
解答 解:(1)∵矩形EFGH,AD是高,
∴MD=HE=x,HG∥BC,
∴AM=AD-MD=120-x,△AHG∽△ABC,
∴$\frac{AM}{AD}$=$\frac{HG}{BC}$,
即$\frac{120-x}{120}$=$\frac{y}{160}$,
∴y=-$\frac{4}{3}$x+160;
(2)矩形EFGH的面积S=xy=x(-$\frac{4}{3}$x+160),
=-$\frac{4}{3}$x2+160x,
=-$\frac{4}{3}$(x2-120x+3600)+4800,
=-$\frac{4}{3}$(x-60)2+4800,
所以,当x=60时,S取最大值4800.
点评 本题考查了相似三角形的应用,矩形的性质,二次函数的最值问题,主要利用了相似三角形对应高的比等于相似比,(2)将二次函数解析式整理出顶点式形式求解更简便.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
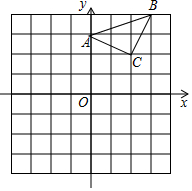 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.
如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com