
某旅游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t (时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:

(1)求该团去景点时的平均速度是多少?
(2)该团在旅游景点游玩了多少小时?
(3)求出返程途中S(千米)与时间t (时)的函数关系式,并求出自变量t的取值范围.
(1)90千米/时;(2)4小时;(3)设S=-60t+1020(14≤t≤17)
【解析】
试题分析:(1)根据图象提供的有关信息结合路程、速度、时间的关系即可求得结果;
(2)直接根据图象提供的有关信息即可求得结果;
(3)设返回途中S(千米)与时间t (时)的函数关系式为S=kt+b,根据待定系数法即可求得结果.
(1)180÷(10-8)=90(千米/时)
所以该团去景点时的平均速度是90千米/时;
(2)14-10=4(小时)
该团在旅游景点游玩了4小时;
(3)设返回途中S(千米)与时间t (时)的函数关系式为S=kt+b,
根据题意得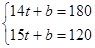 ,
,
解得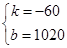 ,
,
因此其关系式为S=-60t+1020,自变量t的取值范围14≤t≤17.
考点:一次函数的应用
点评:解答本题的关键是读懂题意及图形特征,同时熟练掌握待定系数法求函数关系式.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
 的关系可以用下的折线表示.根据图象提供的有关信息,解答下列问题:
的关系可以用下的折线表示.根据图象提供的有关信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 某旅游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t (时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
某旅游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t (时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省大丰市第四中学八年级上学期期末考试数学试卷(带解析) 题型:解答题
某旅游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t (时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题: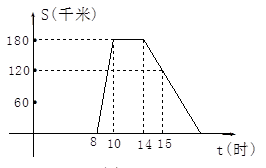
(1)求该团去景点时的平均速度是多少?
(2)该团在旅游景点游玩了多少小时?
(3)求出返程途中S(千米)与时间t (时)的函数关系式,并求出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
 某旅
某旅![]() 游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t (时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
游团上午8时从旅馆出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离旅馆的距离S(千米)与时间t (时)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
(1)求该团去景点时的平均速度是多少?
(2)该团在旅游景点游玩了多少小时?
(3)求出返程途中S(千米)与时间t (时)的
函数关系式,并求出自变量t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com