
 正方形ABCD中,点E在边BC上,CE=2EB,连接AE、BD交于点F,∠DAE的角平分线交DC于点H,交BD于点M,将△MAD沿AD翻折得到△NAD,连接NF、NH、FH,若AB=3,则△NFH面积为$\frac{183}{8}$-6$\sqrt{10}$.
正方形ABCD中,点E在边BC上,CE=2EB,连接AE、BD交于点F,∠DAE的角平分线交DC于点H,交BD于点M,将△MAD沿AD翻折得到△NAD,连接NF、NH、FH,若AB=3,则△NFH面积为$\frac{183}{8}$-6$\sqrt{10}$. 分析 如图,延长CB到P,使得BP=DH,连接AP,作FQ⊥AB于Q交CD于W,作NT⊥CD于T.则四边形BCWQ是矩形,△ABP≌△ADH.首先证明AE=BE+DH,根据S△NFH=S四边形FHTM-S△DHN=S△DNF+S△FDH-S△DHN,只要求出DN、DF、DH、NT、FW、DW即可解决问题.
解答 解:如图,延长CB到P,使得BP=DH,连接AP,作FQ⊥AB于Q交CD于W,作NT⊥CD于T.则四边形BCWQ是矩形,△ABP≌△ADH.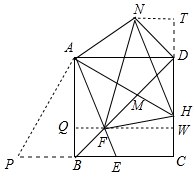
∵正方形ABCD中,AB=3,
∴BC=AD=CD=3,BD=3$\sqrt{2}$,
∵CE=2EB,
∴CE=2,BE=1,
∴AE=$\sqrt{10}$,
∵AD∥BE,BQ∥DW,
∴$\frac{BF}{FD}$=$\frac{BE}{AD}$=$\frac{EF}{AF}$=$\frac{1}{3}$=$\frac{FQ}{FW}$,
∴BF=$\frac{3\sqrt{2}}{4}$,DF=$\frac{9\sqrt{2}}{4}$,QF=$\frac{3}{4}$,FW=$\frac{9}{4}$,EF=$\frac{\sqrt{10}}{4}$,AF=$\frac{3\sqrt{10}}{4}$,
∵∠MAD=∠MAF,
∴$\frac{AD}{AF}$=$\frac{DM}{FM}$(角平分线的性质定理),
∴$\frac{3}{\frac{3\sqrt{10}}{4}}$=$\frac{DM}{MF}$,
∵DM+MF=$\frac{9\sqrt{2}}{4}$,
∴DM=$\frac{9\sqrt{2}}{4+\sqrt{10}}$,
由翻折可知,DN=DM=$\frac{9\sqrt{2}}{4+\sqrt{10}}$,
∵△ABP≌△ADH,
∴∠PAB=∠DAH=∠HAF,∠P=∠AHD
∵∠AHD=∠BAH=∠BAE+∠HAF=∠BAE+∠PAB=∠PAE,
∴∠P=∠PAE,
∴AE=EP=PB+BE=DH+BE,
∴DH=$\sqrt{10}$-1,
∵∠ADB=∠NDA=45°,
∴∠NDF=90°=∠ADC,
∴∠NDT+∠BDC=90°,∵∠BDC+∠CBD=90°,
∴∠NDT=∠DBC,
∵∠T=∠FWD=90°,
∴△DNT∽△FDW,
∴$\frac{NT}{DW}$=$\frac{DN}{DF}$,
∴$\frac{NT}{\frac{9}{4}}$=$\frac{\frac{9\sqrt{2}}{4+\sqrt{10}}}{\frac{9\sqrt{2}}{4}}$,
∴NT=$\frac{9}{4+\sqrt{10}}$,
∴S△NFH=S四边形FHTM-S△DHN=S△DNF+S△FDH-S△DHN=$\frac{1}{2}$•$\frac{9\sqrt{2}}{4+\sqrt{10}}$•$\frac{9\sqrt{2}}{4}$+$\frac{1}{2}$•($\sqrt{10}$-1)•$\frac{9}{4}$-$\frac{1}{2}$•($\sqrt{10}$-1)•$\frac{9}{4+\sqrt{10}}$=$\frac{183}{8}$-6$\sqrt{10}$.
点评 本题考查翻折变换、正方形的性质、角平分线的性质定理(可以用面积证明)、平行线分线段成比例定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,本题计算量比较大,有一定的难度,证明AE=BE+DH是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,B是线段AD上一动点,沿A→D→A以每秒2cm的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(t不超过10秒)
如图,B是线段AD上一动点,沿A→D→A以每秒2cm的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(t不超过10秒)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,-2 | B. | 4,1 | C. | 2,1 | D. | 4,-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{1}$,$\sqrt{2}$,$\sqrt{3}$ | B. | 7,24,25 | C. | 6,8,10 | D. | 1,2,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
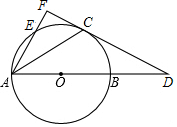 如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD=∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.
如图,AB是⊙O的直径,C为⊙O上一点,经过点C的直线与AB的延长线交于点D,连接AC,BC,∠BCD=∠CAB.E是⊙O上一点,弧CB=弧CE,连接AE并延长与DC的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 39.8×105 | B. | 3.98×106 | C. | 3.98×107 | D. | 0.398×107 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com