
如果一元二次方程ax2+bx+c=0的两根x1、x2均为正数,且满足1< <2(其中x1>x2),那么称这个方程有“邻近根”.
<2(其中x1>x2),那么称这个方程有“邻近根”.
(1)判断方程 是否有“邻近根”,并说明理由;
是否有“邻近根”,并说明理由;
(2)已知关于x的一元二次方程mx2-(m-1)x-1=0有“邻近根”,求m的取值范围.
(1) 方程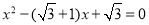 有“邻近根”;理由见解析;(2)-2<m<-1或-1<m<
有“邻近根”;理由见解析;(2)-2<m<-1或-1<m<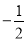 .
.
【解析】
试题分析:(1)先解方程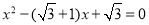 得到x1=
得到x1=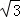 ,x2=1,则满足1<
,x2=1,则满足1<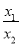 <2,所以可判断方程
<2,所以可判断方程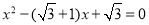 有“邻近根”;
有“邻近根”;
(2)根据判别式的意义得到m≠0且△=(m-1)2-4m×(-1)=(m+1)2≥0,利用求根公式解得x1=1,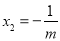 或
或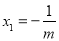 ,x2=1,则m<0,然后讨论:
,x2=1,则m<0,然后讨论:
若x1=1,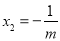 ,则
,则 ,
,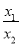 是关于m的正比例函数,根据正比例函数性质得到-2<m<-1;
是关于m的正比例函数,根据正比例函数性质得到-2<m<-1;
若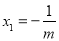 ,x2=1,则
,x2=1,则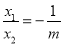 ,
,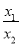 是关于m的反比例函数,根据反比例函数性质得-1<m<
是关于m的反比例函数,根据反比例函数性质得-1<m<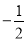 ,最后综合得到m的取值范围.
,最后综合得到m的取值范围.
试题解析:(1)方程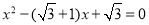 有“邻近根”.理由如下:
有“邻近根”.理由如下:
∵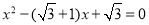 ,
,
∴(x-1)(x-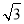 )=0,
)=0,
∵x1>x2,
∴x1=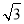 ,x2=1,
,x2=1,
这时x1>0,x2>0,且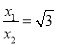 ,
,
∵1<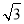 <2,
<2,
∴满足1<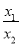 <2,
<2,
∴方程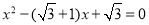 有“邻近根”;
有“邻近根”;
(2)由已知m≠0且△=(m-1)2-4m×(-1)=(m+1)2≥0,
∴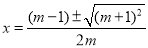
∴x1=1,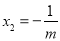 或
或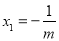 ,x2=1,
,x2=1,
∵一元二次方程ax2+bx+c=0有“邻近根”,
∴x1、x2均为正数,
∴m<0
若x1=1,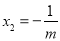 ,则
,则 ,
,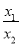 是关于m的正比例函数,
是关于m的正比例函数,
∵-1<0,
∴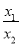 随m的增大而减小.
随m的增大而减小.
当1<-m<2时,
∴-2<m<-1;
若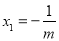 ,x2=1,则
,x2=1,则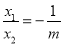 ,
,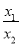 是关于m的反比例函数,
是关于m的反比例函数,
∵-1<0,
∴在第二象限,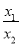 随m的增大而增大.
随m的增大而增大.
当1<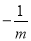 <2时,
<2时,
∴-1<m<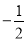 .
.
综上,m的取值范围是-2<m<-1或-1<m<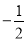 .
.
考点:1.根的判别式;2.解一元二次方程-公式法;3.解一元二次方程-因式分解法;4.正比例函数的性质;5.反比例函数的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年辽宁省盘锦市中考第一次模拟考试数学试卷(解析版) 题型:选择题
要调查下列问题,你认为哪些适合抽样调查()
①市场上某种食品的某种添加剂的含量是否符合国家标准;
②检测某地区空气的质量;
③调查全市中学生一天的学习时间.
A.①② B.①③ C.②③ D.①②③
查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:填空题
小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径OB=3cm,高OC=4cm,则这个圆锥漏斗的侧面积是 cm2.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年辽宁省丹东市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
一家鞋店在一段时间内销售了某种男鞋200双,各种尺码鞋的销售量如下表所示:
尺码/厘米 | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 |
销售量/双 | 5 | 10 | 22 | 39 | 56 | 43 | 25 |
一般来讲,鞋店老板比较关心哪种尺码的鞋最畅销,也就是关心卖出的鞋的尺码组成的一组数据的( ) A.平均数 B.中位数 C.众数 D.方差
查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省厦门市业质量检查数学试卷(解析版) 题型:解答题
如图,在梯形ABCD中,AB∥CD,BD⊥AD,BC=CD,∠A=60°,CD=2cm.
(1)求∠CBD的度数;
(2)求下底AB的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省长沙市长郡教育集团九年级期末考试数学试卷(解析版) 题型:填空题
如图,四边形OABC是边长为1的正方形,反比例函数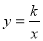 的图象过点B,则
的图象过点B,则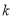 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com