
科目:初中数学 来源: 题型:
阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。
对于任意正实数a、b,可作如下变形a+b=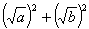 =
=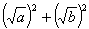 -
-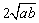 +
+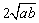 =
=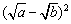 +
+ 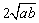 ,
,
又∵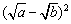 ≥0, ∴
≥0, ∴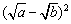 +
+ 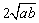 ≥0+
≥0+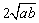 ,即
,即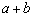 ≥
≥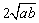 .
.
(1)根据上述内容,回答下列问题:在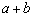 ≥
≥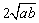 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥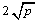 ,当且仅当a、b满足 时,a+b有最小值
,当且仅当a、b满足 时,a+b有最小值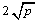 .
.
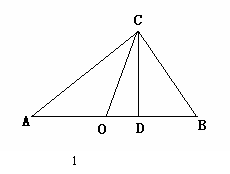
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a,DB=2b, 试根据图形验证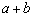 ≥
≥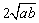 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
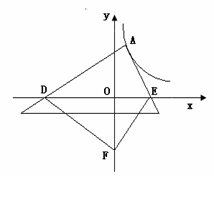
(3)探索应用:如图2,已知A为反比例函数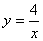 的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的盒子里装有6个分别写有数字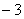 ,
,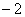 ,
, ,0,1,2,的小球,它们除数字不同外其余全部相同。现从盒子里随机取出一个小球,记下数字
,0,1,2,的小球,它们除数字不同外其余全部相同。现从盒子里随机取出一个小球,记下数字 后不放回,再取出一个记下数字
后不放回,再取出一个记下数字 ,那么点
,那么点 在抛物线
在抛物线 上的概率是( )
上的概率是( )
A. B.
B. C.
C. D.
D.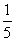
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,已知二次函数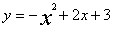 与坐标轴分别交于A、D、B三点,顶点为C。
与坐标轴分别交于A、D、B三点,顶点为C。
(1)求tan∠BAC
(2)在y轴上是否存在一点P,使得△DOP与△ABC相似,如果存在,求出点P的坐标,如果不存在,说明理由。
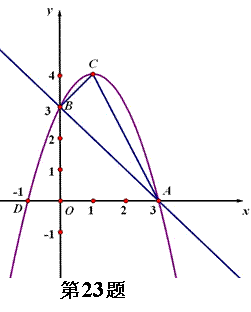 (3)Q是抛物线上一动点,使得以A、B、C、Q为端点的四边形是一个梯形,请直接写出满足条件的Q点的坐标。(不要求写出解题过程)
(3)Q是抛物线上一动点,使得以A、B、C、Q为端点的四边形是一个梯形,请直接写出满足条件的Q点的坐标。(不要求写出解题过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com