
【题目】解下列各题:
(1)已知∠A,∠B,∠C是锐角三角形ABC的三个内角,且满足(2sinA-![]() )2+
)2+![]() =0,求∠C的度数;
=0,求∠C的度数;
(2)已知tanα的值是方程x2-x-2=0的一个根,求式子![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点,AB为腰在第三象限作等腰直角△ABC.

(1)求C点的坐标.
(2)如图2,OA=2,P为y轴负半轴上的一个动点,若以P为直角顶点,PA为腰作等腰直角△APD,过D作DE⊥x轴于E点,求OP-DE的值.
(3)如图3,点F坐标为(-4,-4),点G(0,m)在y轴负半轴,点H(n,0)在x轴的正半轴,且FH⊥FG,求m+n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
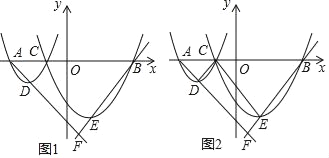
【题目】如图1,在平面直角坐标系xOy中,已知A、B两点的坐标分别为(﹣4,0)、(4,0),C(m,0)是线段AB上一动点(与A、B两点不重合),抛物线l1:y=ax2+b1x+c1(a>0)经过点A、C,顶点为D,抛物线l2:y=ax2+b2x+c2(a>0)经过点C、B,顶点为E,直线AD、BE相交于F.
(1)若a=![]() ,m=﹣1,求抛物线l1、l2的解析式;
,m=﹣1,求抛物线l1、l2的解析式;
(2)若a=1,∠AFB=90°,求m的值;
(3)如图2,连接DC、EC,记△DAC的面积为S1,△ECB的面积为S2,△FAB的面积为S,问是否存在点C使得2S1S2=aS,若存在,请求出C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,CD、CE分别是△ABC的高和角平分线,∠BAC=α,∠B=β(α>β).

(1)若α=70°,β=40°,求∠DCE的度数;
(2)试用α、β的代数式表示∠DCE的度数(直接写出结果);
(3)如图②,若CE是△ABC外角∠ACF的平分线,交BA延长线于点E,且α﹣β=30°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题:例题: 已知二次三项式x2 4x m 有一个因式是 ( x 3) ,求另一个因式以及 m 的值.
解:设另一个因式为 ( x n) ,得x2 4x m ( x 3) ( x n)
则x2 4 x m x2 (n 3) x 3n
∴![]()
解得: n 7, m 21
∴ 另一个因式为 ( x 7) , m 的值为-21 .
问题:仿照以上方法解答下面问题:
(1)已知二次三项式2x2+3x-k有一个因式是(2x-5),求另一个因式以及k的值.
(2)已知二次三项式6x2+4ax+2有一个因式是(2x+a),a是正整数,求另一个因式以及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
(1)甲船从C处出发追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是过点
是过点![]() 的一条直线,且点
的一条直线,且点![]() 在线段
在线段![]() 上时,
上时,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .易证:
.易证:![]() .
.

(1)如图②,点![]() 在线段
在线段![]() 的延长线时,其余条件不变,问
的延长线时,其余条件不变,问![]() 与
与![]() ,
,![]() 的关系如何?请证明;
的关系如何?请证明;
(2)如图③,点![]() 在线段
在线段![]() 的延长线时,其余条件不变,问
的延长线时,其余条件不变,问![]() 与
与![]() 的关系如何?请直接写出结果,不需证明.
的关系如何?请直接写出结果,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图, △ABC中,AB=AC,D在AC上,E在BC上,A E,B D交于F,∠AFD=60°,∠FDC+∠FEC=180°.

(1)求证:BE=CD.
(2)如图2,过点D作DG⊥AF于G,直接写出AE ,FG, BF的关系.
(3)如图3,在(2)的条件下,连接CG,若FG=BF,△AGD的面积等于5,求GC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边AB,AD分别在等腰直角△AEF的腰AE,AF上,点C在△AEF内,则有DF=BE(不必证明).将正方形ABCD绕点A逆时针旋转一定角度α(0°<α<90°)后,连接BE,DF.请在图2中用实线补全图形,这时DF=BE还成立吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com