
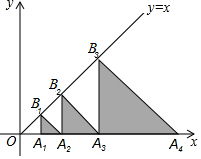
 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA1=1,则△B2016A2016A2017的面积为24029.
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA1=1,则△B2016A2016A2017的面积为24029. 分析 由OA1=1结合一次函数图象上点的坐标特征可得出A1B1=1,根据等腰直角三角形的性质即可得出AnAn+1=2n-1,依此规律可得出A2016A2017=22015,再根据三角形的面积即可求出结论.
解答 解:∵OA1=1,B1在直线y=x上,
∴A1B1=1.
∵△A1B1A2,△A2B2A3,…,△AnBnAn+1都是等腰直角三角形,
∴A1A2=1,
∴OA2=2,A2A3=2.
进而得出A3A4=4,A4A5=8,A5A6=16,
∴AnAn+1=2n-1,
∴A2016A2017=22015,
∴${S}_{△{B}_{2016}{A}_{2016}{A}_{2017}}$=$\frac{1}{2}$(A2016A2017)2=24029.
故答案为:24029.
点评 本题考查了一次函数图象上点的坐标特征、等腰直角三角形以及规律型中数的变化,根据线段的变化找出AnAn+1=2n-1是解题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
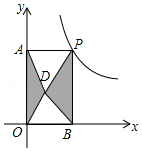 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是3.
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
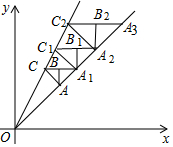 如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为$\frac{{4}^{n}}{{3}^{n+1}}$.
如图,在平面直角坐标系第一象限内,直线y=x与直线y=2x的内部作等腰Rt△ABC,是∠ABC=90°,边BC∥x轴,AB∥y轴,点A(1,1)在直线y=x上,点C在直线y=2x上:CB的延长线交直线y=x于点A1,作等腰Rt△A1B1C1,是∠A1B1C1=90°,B1C1∥x轴,A1B1∥y轴,点C1在直线y=2x上…按此规律,则等腰Rt△AnBnCn的腰长为$\frac{{4}^{n}}{{3}^{n+1}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
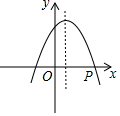 如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.
如图,抛物线y=ax2+bx+c(a<0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(3,0)在该抛物线上,则a-b+c的值为0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
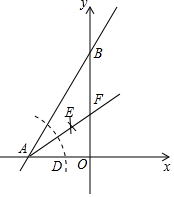 如图,在平面直角坐标系中,一次函数y=$\sqrt{3}$x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )
如图,在平面直角坐标系中,一次函数y=$\sqrt{3}$x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
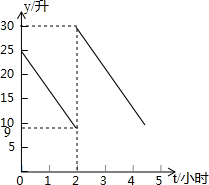 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
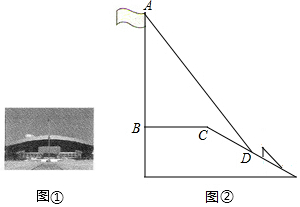 深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°.1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.
深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°.1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com