
 如图所示,一只老鼠沿A→B→D的路线逃跑,一只猫同时从阶梯(折线)沿A→C→D的路线去追,结果在距离C点0.6米的D处,猫捉住了老鼠.已知老鼠的速度是猫的
如图所示,一只老鼠沿A→B→D的路线逃跑,一只猫同时从阶梯(折线)沿A→C→D的路线去追,结果在距离C点0.6米的D处,猫捉住了老鼠.已知老鼠的速度是猫的| 11 |
| 14 |
| 设梯级(折线)A→C的长度为 | xm | ||||
| AB+BC的长度为 | x x | ||||
| A→C→D的长度为 | x+0.6 x+0.6 | ||||
| A→B→D的长度为 | x-0.6 x-0.6 | ||||
| 设猫捉住老鼠所用时间为 | ts | ||||
| 猫的速度是 |
| ||||
| 老鼠的速度是 |
|
| x+0.6 |
| t |
| x-0.6 |
| t |
| 11 |
| 14 |
| 设梯级(折线)A→C的长度为 | xm | ||
| AB+BC的长度为 | xm | ||
| A→C→D的长度为 | (x+0.6)m | ||
| A→B→D的长度为 | (x-0.6)m | ||
| 设猫捉住老鼠所用时间为 | ts | ||
| 猫的速度是 |
| ||
| 是 |
|
| 11 |
| 14 |
| x+0.6 |
| t |
| 11 |
| 14 |
| x-0.6 |
| t |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
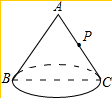 如图所示,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一只老鼠正在偷吃粮食.此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是多少米?(结果不取近似值)
如图所示,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一只老鼠正在偷吃粮食.此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是多少米?(结果不取近似值)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
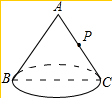
 如图所示,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一只老鼠正在偷吃粮食.此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是多少米?(结果不取近似值)
如图所示,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一只老鼠正在偷吃粮食.此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是多少米?(结果不取近似值)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com