Question

【题目】如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积．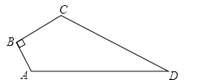

Answer 1

【答案】解：连接AC，如图所示：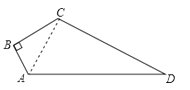

∵∠B=90°，
∴△ABC为直角三角形，
又∵AB=3，BC=4，
∴根据勾股定理得：AC==5，
又∵CD=12，AD=13，
∴AD2=132=169，CD2+AC2=122+52=144+25=169，
∴CD2+AC2=AD2 ，
∴△ACD为直角三角形，∠ACD=90°，
则S四边形ABCD=S△ABC+S△ACD=ABBC+ACCD=×3×4+×5×12=36．
故四边形ABCD的面积是36．
【解析】连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．