练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
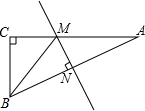
    2．如图，在Rt△ABC中，∠C=90°，AC=12，AB=13，AB边的垂直平分线分别交AB、AC于N、M两点，则△BCM的周长为（　　）
    A．18B．16C．17D．无法确定

    分析 根据勾股定理求出BC的长，根据线段垂直平分线的性质得到MB=MA，根据三角形的周长的计算方法代入计算即可．

    解答 解：在Rt△ABC中，∠C=90°，AC=12，AB=13，
    由勾股定理得，BC=5，
    ∵MN是AB的垂直平分线，
    ∴MB=MA，
    △BCM的周长=BC+CM+MB=BC+CM+MA=BC+CA=17，
    故选：C．

    点评 本题考查的是线段的垂直平分线的性质等几何知识，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．某冷饮点一天售出各种口味雪糕数量的扇形统计图如图所示，其中售出红豆口味的雪糕200支．
    （1）售出的雪糕总量是多少？
    （2）水果口味的雪糕售出后了多少支？
    （3）若绿豆数量所占比例为12%，那么巧克力口味的雪糕售出了多少支？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

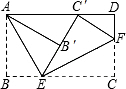    13．将矩形ABCD按如图所示的方式折叠，AE、EF为折痕，∠BAE=30°，AB=$\sqrt{3}$，折叠后，点C落在AD边上的C′处，并且点B落在EC′边上的B′处，则BC的长为（　　）
    A．$\sqrt{3}$B．2$\sqrt{3}$C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

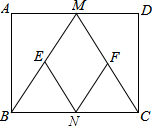    10．如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是边BM、CM的中点，当AB：AD=1：2时，四边形MENF是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．不等式组$\left\{\begin{array}{l}{2x-5≥-3}\\{3-x≥-1}\end{array}\right.$的整数解的个数是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列能用平方差公式计算的是（　　）
    A．（-x+y）（x-y）B．（y-1）（-1-y）C．（x-2）（x+1）D．（2x+y）（2y-x）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

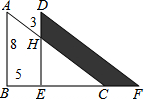    14．如图，原来是重叠的两个直角三角形，将其中一个三角形沿着BC方向平移线段BE的距离，就得到此图形，下列结论正确的有（　　）
    ①AC∥DF；②HE=5；③CF=5；④阴影部分面积为$\frac{55}{2}$．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．已知9.972=99.4009，9.982=99.6004，9.992=99.8001，$\sqrt{997000}$之值的个位数字为8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．（1）解方程组：$\left\{\begin{array}{l}{3x-5y=3}\\{\frac{x}{2}-\frac{y}{3}=1}\end{array}\right.$
    （2）解不等式组，并将解集在数轴上表示出来．
    $\left\{\begin{array}{l}{\frac{x+2}{3}＜1}\\{2（1-x）≤5}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案