练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图的圆柱的高为5cm，主视图的面积为30cm2，则圆柱的俯视图的面积为


    1. A.
      9xcm2
    2. B.
      18xcm2
    3. C.
      30xcm2
    4. D.
      36cm2
    A
    分析：根据主视图的面积=圆柱的直径×圆柱的高可得圆柱的底面直径，圆柱的俯视图为圆，面积等于π×半径2，把相关数值代入即可求解．
    解答：∵圆柱的高为5cm，主视图的面积为30cm2，
    ∴圆柱的底面直径为30÷5=6cm，
    ∴圆柱的俯视图的面积=π×（6÷2）2=9πcm2．
    故选A．
    点评：用到的知识点为：圆柱的主视图反映圆柱的高与底面直径；俯视图是圆，反映圆柱的底面直径．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    研究课题：蚂蚁怎样爬最近？
    研究方法：如图1，正方体的棱长为5cm，一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处，要求该蚂蚁需要爬行的最短路程的长，可将该正方体右侧面展开，由勾股定理得最短路程的长为AC1=
    		AC2+CC12
    =
    		102+52
    =5
    		5
    cm．这里，我们将空间两点间最短路程问题转化为平面内两点间距离最短问题．
    研究实践：（1）如图2，正四棱柱的底面边长为5cm，侧棱长为6cm，一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处，蚂蚁需要爬行的最短路程的长为
     
    ．
    （2）如图3，圆锥的母线长为4cm，圆锥的侧面展开图如图4所示，且∠AOA1=120°，一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A．求该蚂蚁需要爬行的最短路程的长．
    （3）如图5，没有上盖的圆柱盒高为10cm，底面圆的周长为32cm，点A距离下底面3cm．一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处．请求出蚂蚁需要爬行的最短路程的长．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

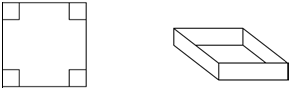    小明用一块正方形纸板，剪去角上四个小正方形后做成一个无盖纸盒（如图），纸盒高为5cm，容积为405cm2，则这块正方形纸板的边长为
    19cm
    19cm
    ．

    查看答案和解析>>

    科目：初中数学 来源：2011年初中毕业升学考试（贵州黔南州卷）数学 题型：选择题

    如图，圆柱的底面周长为6cm，AC是底面圆的直径，高BC=6cm，点P是母线BC上一点，且PC=BC．一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是（　　）

     A、㎝

     B、5cm

     C、㎝

     D、7cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    小明用一块正方形纸板，剪去角上四个小正方形后做成一个无盖纸盒（如图），纸盒高为5cm，容积为405cm2，则这块正方形纸板的边长为________．

    查看答案和解析>>

    科目：初中数学 来源：鼓楼区二模 题型：解答题

    研究课题：蚂蚁怎样爬最近？
    研究方法：如图1，正方体的棱长为5cm，一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处，要求该蚂蚁需要爬行的最短路程的长，可将该正方体右侧面展开，由勾股定理得最短路程的长为AC1=
    		AC2+CC12
    =
    		102+52
    =5
    		5
    cm．这里，我们将空间两点间最短路程问题转化为平面内两点间距离最短问题．
    研究实践：（1）如图2，正四棱柱的底面边长为5cm，侧棱长为6cm，一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处，蚂蚁需要爬行的最短路程的长为______．
    （2）如图3，圆锥的母线长为4cm，圆锥的侧面展开图如图4所示，且∠AOA1=120°，一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A．求该蚂蚁需要爬行的最短路程的长．
    （3）如图5，没有上盖的圆柱盒高为10cm，底面圆的周长为32cm，点A距离下底面3cm．一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处．请求出蚂蚁需要爬行的最短路程的长．
    精英家教网

    查看答案和解析>>

    同步练习册答案