
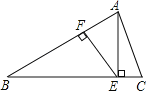
【题目】已知:如图,等腰△ABC中,AB=BC,AE⊥BC于点E,EF⊥AB于点F,若CE=1,![]() ,求EF的长.
,求EF的长.
【答案】![]()
【解析】
试题分析:Rt△ABE中,EF⊥AB,易得∠AEF=∠B,即cos∠B=![]() ,由此可求得BE、AB的比例关系,即BE、BC的比例关系,根据EC=BC﹣BE,即可求出BE、AE的长;然后根据∠AEF的余弦值,即可在Rt△AEF中,求出EF的长.
,由此可求得BE、AB的比例关系,即BE、BC的比例关系,根据EC=BC﹣BE,即可求出BE、AE的长;然后根据∠AEF的余弦值,即可在Rt△AEF中,求出EF的长.
解:∵AE⊥BC,∴∠AEF+∠1=90°;
∵EF⊥AB,∴∠1+∠B=90°;
∴∠B=∠AEF;
∴![]()
∵在Rt△ABE中,∠AEB=90°
∴![]() ;
;
设BE=4k,AB=5k,∵BC=AB,∴EC=BC﹣BE=BA﹣BE=k;
∵EC=1,∴k=1;
∴BE=4,AB=5;
∴AE=3;(4分)
在Rt△AEF中,∠AFE=90°,
∵![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】太仓港区道路绿化工程工地有大量货物需要运输,某车队有载重量为8吨和10吨的卡车共15辆,所有车辆运输一次能运输128吨货物.
(1)求该车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的扩大,车队需要一次运输货物170吨以上,为了完成任务,车队准备增购这两种卡车共5辆(两种车都购买),请写出所有可能的购车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
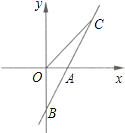
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张数学竞赛练习卷,只有25道选择题,做对一道给4分,做错一道扣1分,某同学全部做完练习,共得70分,问他一共对了_________道题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com