
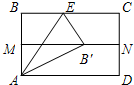
 将矩形纸片ABCD对折,得折痕MN,再把点B叠在折痕MN上,得折痕AE,若AB=
将矩形纸片ABCD对折,得折痕MN,再把点B叠在折痕MN上,得折痕AE,若AB= ,则折痕AE的长为
,则折痕AE的长为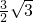
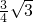

 ,∠BAE=∠B′AE,∠B=∠EB′A=90°,那么在Rt△AEB′中,AH=EH=B′H,得出∠EAB′=∠HB′A,根据平行线的性质推出∠DAB′=∠HB′A,通过等量代换可推出∠B′AE=∠EAB=B′AD=30°,最后根据特殊角的三角函数值即可推出AE的长度.
,∠BAE=∠B′AE,∠B=∠EB′A=90°,那么在Rt△AEB′中,AH=EH=B′H,得出∠EAB′=∠HB′A,根据平行线的性质推出∠DAB′=∠HB′A,通过等量代换可推出∠B′AE=∠EAB=B′AD=30°,最后根据特殊角的三角函数值即可推出AE的长度.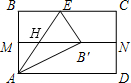 解:如图,设MN和AE交于点H,
解:如图,设MN和AE交于点H, ,
, ,∠BAE=∠B′AE,∠B=∠EB′A=90°,
,∠BAE=∠B′AE,∠B=∠EB′A=90°, ,∠BAE=30°,
,∠BAE=30°,

科目:初中数学 来源: 题型:
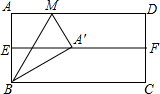 如图,将矩形纸片ABCD对折一次,使边AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF的A′处并使折痕经过点B,得到折痕BM,则∠CBA′=
如图,将矩形纸片ABCD对折一次,使边AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF的A′处并使折痕经过点B,得到折痕BM,则∠CBA′=查看答案和解析>>
科目:初中数学 来源:2013届江西省景德镇市九年级第三次质检数学试卷(带解析) 题型:单选题
如图,将矩形纸片ABCD对折的,使点B与点D重合,折痕为EF,连结BE,则与线段BE相等的线段条数(不包括BE,不添加辅助线)有( )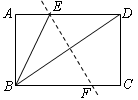
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江西省景德镇市九年级第三次质检数学试卷(解析版) 题型:选择题
如图,将矩形纸片ABCD对折的,使点B与点D重合,折痕为EF,连结BE,则与线段BE相等的线段条数(不包括BE,不添加辅助线)有( )
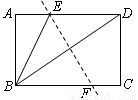
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com