(1)已知一元二次方程x2+px+q=0(p2-4q≥0)的两根为x1、x2;求证:x1+x2=-p,x1•x2=q.
(2)已知抛物线y=x2+px+q与x轴交于A、B两点,且过点(-1,-1),设线段AB的长为d,当p为何值时,d2取得最小值,并求出最小值.
【答案】
分析:(1)先根据求根公式得出x
1、x
2的值,再求出两根的和与积即可;
(2)把点(-1,-1)代入抛物线的解析式,再由d=|x
1-x
2|可知d
2=(x
1-x
2)
2=(x
1+x
2)
2-4 x
1•x
2=p
2,再由(1)中 x
1+x
2=-p,x
1•x
2=q即可得出结论.
解答:证明:(1)∵a=1,b=p,c=q
∴△=p
2-4q
∴x=
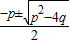
即x
1=
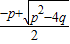
,x
2=
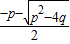
∴x
1+x
2=
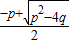
+
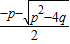
=-p,
x
1•x
2=
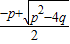
•
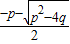
=q;
(2)把(-1,-1)代入y=x
2+px+q得1-p+q=-1,
所以,q=p-2,
设抛物线y=x
2+px+q与x轴交于A、B的坐标分别为(x
1,0)、(x
2,0)
∵d=|x
1-x
2|,
∴d
2=(x
1-x
2)
2=(x
1+x
2)
2-4x
1•x
2=p
2-4q=p
2-4p+8=(p-2)
2+4
当p=2时,d
2的最小值是4.
点评:本题考查的是抛物线与x轴的交点及根与系数的关系,熟知x
1,x
2是方程x
2+px+q=0的两根时,x
1+x
2=-p,x
1x
2=q是解答此题的关键.

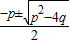 即x1=
即x1=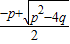 ,x2=
,x2=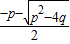
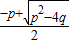 +
+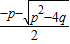 =-p,
=-p,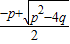 •
•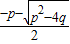 =q;
=q;
