
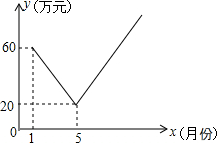
 保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2016年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月利润60万元逐月等额下降,到5月份利润为20万元.5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.
保护生态环境,实行“节能减排”的理念已深入人心.我市某工厂从2016年1月开始,进行机器设备更新,产业转型换代的改造,改造期间利润明显下降,从1月利润60万元逐月等额下降,到5月份利润为20万元.5月底改造完成,从这时起,该厂每个月的利润都比上个月增加15万元.设第x个月的利润为y(万元),函数图象如图.分析 (1)根据函数图象和图象中的数据可以求得相应的函数解析式;
(2)根据(1)中的函数解析式,将y=50代入函数解析式中,即可解答本题.
解答 解:(1)设当1≤x≤5时,y与x的函数关系式为y=kx+b,
$\left\{\begin{array}{l}{k+b=60}\\{5k+b=20}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-10}\\{b=70}\end{array}\right.$,
即当1≤x≤5时,y与x的函数关系式为y=-10x+70,
设当x>5时,y与x的函数关系式为y=mx+n,
$\left\{\begin{array}{l}{5m+n=20}\\{6m+n=35}\end{array}\right.$,得$\left\{\begin{array}{l}{m=15}\\{n=-55}\end{array}\right.$,
即当x>5时,y与x的函数关系式为y=15x-55,
答:改造期间y与x的函数关系式是y=-10x+70,改造完成后y与x的函数关系式是y=15x-55;
(2)将y=50代入y=-10x+70,得x=2,
将y=50代入y=15x-55,得x=7,
答:该厂2月份和7月份的利润为50万元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用一次函数的性质和数形结合的思想解答.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x-5 | B. | y=x-10 | C. | y=-x-5 | D. | y=-x-10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
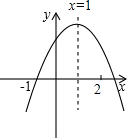 已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有①③④.
已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有①③④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com