
在正实数范围内,只存在一个数是关于x的方程 的解,则实数k的取值范围是 .
的解,则实数k的取值范围是 .
 或
或 或
或
【解析】
试题分析:先把原方程化为2x2-3x-(k+3)=0,一定是一个一元二次方程,在正实数范围内,只存在一个数是关于x的方程的解,因而可能方程有两个相同的实根,求得即可进行判断;或解方程得到的两个根中有一个是方程的增根,即x=1是方程2x2-3x-(k+3)=0的解,即可求得方程的另一解,然后进行判断;或方程有两个异号得实数根;或其中一根是0,即可求得方程的另一根,进行判断.因而这个方程中再分四种情况讨论:(1)当△=0时;(2)若x=1是方程①的根;(3)当方程①有异号实根时;(4)当方程①有一个根为0时,最后结合题意总结结果即可.
原方程可化为2x2-3x-(k+3)=0,①
(1)当△=0时, ,x1=x2=
,x1=x2= 满足条件;
满足条件;
(2)若x=1是方程①的根,得2×12-3×1-(k+3)=0,k=-4;
此时方程①的另一个根为 ,故原方程也只有一根x=
,故原方程也只有一根x= ;
;
(3)当方程①有异号实根时,x1x2= <0,得k>-3,此时原方程也只有一个正实数根;
<0,得k>-3,此时原方程也只有一个正实数根;
(4)当方程①有一个根为0时,k=-3,另一个根为x=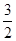 ,此时原方程也只有一个正实根.
,此时原方程也只有一个正实根.
综上所述,满足条件的k的取值范围是 或
或 或
或
考点:方程解的定义,分式的运算,根与系数的关系,根的判别式,解分式方程
点评:本题综合性强,难度较大,是中考常见题,一般出现在选择或填空的最后一题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源:2011-2012学年浙江省杭州市余杭瓶窑学区九年级摸底考试数学试卷(解析版) 题型:解答题
在正实数范围内,只存在一个数是关于 的方程
的方程 的解,求实数
的解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com