
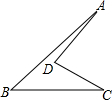
 如图所示是一块空地,AD=
如图所示是一块空地,AD= cm,CD=2cm,AB=5cm,BC=4cm,∠ADC=90°.求这块空地的面积.
cm,CD=2cm,AB=5cm,BC=4cm,∠ADC=90°.求这块空地的面积.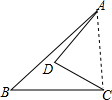 解:连接AC,
解:连接AC, cm,CD=2cm,
cm,CD=2cm, )2+22=9,即AC=3cm,
)2+22=9,即AC=3cm, AC•BC-
AC•BC- DC•AD=
DC•AD= ×3×4-
×3×4- ×2×
×2× =6-
=6- (cm2)
(cm2)

科目:初中数学 来源: 题型:
 某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元?
某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元?查看答案和解析>>
科目:初中数学 来源:1+1轻巧夺冠·优化训练·九年级数学下(北京课改版)·银版 题型:044
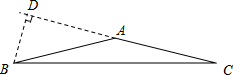
在一新建的立交桥下,有一块如图所示的三角形空地,园林部门要在此空地中间建一个圆形花坛(剩余空地种植草坪),并要求使所建圆形花坛的面积最大,如果你是圆艺师.
(1)请在下面的三角形空地的示意图中,画出你所设计的符合园林部门要求的圆形花坛的示意图.
(2)若△ABC是等腰直角三角形,∠A=90°,斜边BC上的高是![]() +1,求三角形内切圆半径.
+1,求三角形内切圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
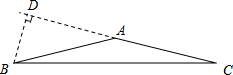 某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元?
某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境,已知AC=30m,AB=20m,∠BAC=150°,这种每平方米的售价是a元,求购买这种草皮至少需要多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com