
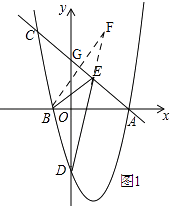
【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0),B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C. 
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标.
【答案】
(1)解:∵抛物线y=ax2+bx﹣4与x轴交于两点A(4,0),B(﹣1,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴此抛物线的解析式为:y=x2﹣3x﹣4
(2)解:如图1,作点B关于直线AC的对称点F,连接DF交AC于点E,
由(1)得,抛物线解析式为y=x2﹣3x﹣4,
∴D(0,﹣4),
∵直线y=﹣x+4交抛物线于点C,
∴ ![]() 解得,
解得, ![]() 或
或 ![]() ,
,
∴C(﹣2,6),
∵A(4,0),
∵直线AC解析式为y=﹣x+4,直线BF⊥AC,且B(﹣1,0),
∴直线BF解析式为y=x+1,
设点F(m,m+1),
∴G( ![]() ,
, ![]() ),
),
∵点G在直线AC上,
∴﹣ ![]() +4=
+4= ![]() ,
,
∴m=4,
∴F(4,5),
∵D(0,﹣4),
∴直线DF解析式为y= ![]() x﹣4,
x﹣4,
解 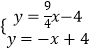 得
得 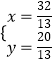
∴直线DF和直线AC的交点E( ![]() ,
, ![]() ).
).
【解析】(1)直接把点A(4,0),B(﹣1,0)代入抛物线y=ax2+bx﹣4求出a、b的值,进而可得出抛物线的解析式;(2)先判断出周长最小时BE⊥AC,即作点B关于直线AC的对称点F,连接DF,交AC于点E,联立方程组即可.
【考点精析】利用抛物线与坐标轴的交点和轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
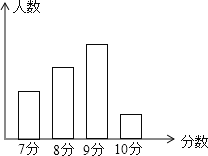
【题目】体育课上,体育老师对七年级一个班的学生进行了立定跳远项目的测试,得到一组测试分数的数据,并将测试所得分数绘制如图所示的统计图,图中从左到右的学生数人数之比为2 : 3 : 4 : 1,且成绩为8分的学生有12人,根据以上信息解答下列问题:
(1) 这个班级有多少名学生?
(2)这组数据的众数是 分,中位数是 分.
(3)这个班级学生立定跳远项目测试的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形(阴影部分)和一个长方形(阴影部分)得到一个“囧”字图案,设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
(1)用含a、x、y的式子表示“囧”的面积;
(2)当a=12,x=7,y=4时,求该图形面积的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题: 
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于x轴对称的△A2B2C2;
(3)点C1的坐标是;点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
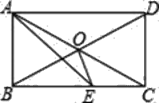
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15° .
(1)求证:△AOB为等边三角形;
(2)求∠BOE度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上. 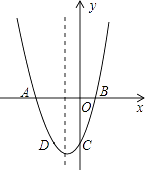
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com