
 与
与 都有实数根,若这两个方程有且只有一个公共根,且
都有实数根,若这两个方程有且只有一个公共根,且 ,则称它们互为“同根轮换方程”.如
,则称它们互为“同根轮换方程”.如 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.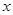 的方程
的方程 与
与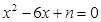 互为“同根轮换方程”,求
互为“同根轮换方程”,求 的值;
的值; 是关于
是关于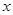 的方程
的方程 的实数根,
的实数根, 是关于
是关于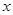 的方程
的方程 的实数根,当
的实数根,当 .
. 分别取何值时,方程
分别取何值时,方程 与
与 互为“同根轮换方程”,请说明理由.
互为“同根轮换方程”,请说明理由. 与
与 互为“同根轮换方程”.
互为“同根轮换方程”. ,先求出公共根,进而求出
,先求出公共根,进而求出 的值;
的值;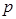 .
. 的取值,只要得到p=q,2a×
的取值,只要得到p=q,2a×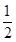 b=ab,即可判断方程
b=ab,即可判断方程 与
与 互为“同根轮换方程”.
互为“同根轮换方程”.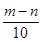 .
. 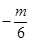 .
.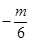 )2+4(
)2+4(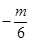 )+m=0.
)+m=0. 有公共根.
有公共根. 解得x=
解得x= .
. 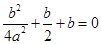 .
.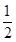 b=ab,
b=ab,  =0互为“同根轮换方程” .
=0互为“同根轮换方程” .

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | 每天的销售量/台 | 每台销售利润/元 |
| 降价前 | 8 | 400 |
| 降价后 | | |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种西瓜,已知西瓜的种植面积的增长率是亩产量的增长率的2倍,今年西瓜的总产量为
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种西瓜,已知西瓜的种植面积的增长率是亩产量的增长率的2倍,今年西瓜的总产量为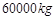 ,求西瓜亩产量的增长率.
,求西瓜亩产量的增长率.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com