
如图所示,(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90°,连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;

(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF=α,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用α表示出直线BE、DF形成的锐角β.
|
(1)证明:延长DF分别交AB、BE于点P、G 1分 在正方形ABCD和等腰直角△AEF中 AD=AB,AF=AE, ∠BAD=∠EAF=90° ∴∠FAD=∠EAB
∴△FAD≌△EAB 2分 ∴∠FDA=∠EBA DF=BE 3分 ∵∠DPA=∠BPG,∠ADP+∠DPA=90° ∴∠EBP+∠BPG=90° ∴∠DGB=90° ∴DF⊥BE 5分 (2)改变.DF=kBE, 证法(一):延长DF交EB的延长线于点H ∵AD=kAB,AF=kAE ∴ ∴ ∵∠BAD=∠EAF= ∴∠FAD=∠EAB ∴△FAD∽△EAB 9分 ∴ ∴DF=kBE 10分 由△FAD∽△EAB得∠AFD=∠AEB ∵∠AFD+∠AFH=180 ∴∠AEB+∠AFH=180° ∵四边形AEHF的内角和为360°, ∴∠EAF+∠EHF=180° ∵∠EAF=
∴ 证法(二):DF=kBE的证法与证法(一)相同 延长DF分别交EB、AB的延长线于点H、G. 由△FAD∽△EAB得∠ADF=∠ABE
∵∠ABE=∠GBH∴∠ADF=∠GBH ∵ 在△ADG中,∠BAD+∠ADF+∠G=180°,∠BAD= ∴ 证法(三):在平行四边形ABCD中AB∥CD可得到∠ABC+∠C=180° ∵∠EBA+∠ABC+∠CBH=180°∴∠C=∠EBA+∠CBH 在 ∴∠EBA+∠CBH+∠CDP=∠CBH+∠BHP ∴∠EBA+∠CDP=∠BHP 由△FAD∽△EAB得∠ADP=∠EBA ∴∠ADP+∠CDP=∠BHP即∠ADC=∠BHP ∵∠BAD+∠ADC=180 ∴ (有不同解法,参照以上给分点,只要正确均得分) |


科目:初中数学 来源: 题型:
 2、如图所示,有一个正方体形的铁丝架,把它的侧棱中点I、J、K、L也用铁丝连上.
2、如图所示,有一个正方体形的铁丝架,把它的侧棱中点I、J、K、L也用铁丝连上.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
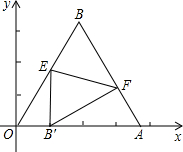 正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.
正方向上,将△OAB折叠,使点B落在边OA上,记为B′,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:
(2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 一轮船正向东以30海里/小时的速度航行,在A点处发现北偏东60°的方向有一小岛C,又航行2小时后,发现小岛C在北偏东30°方向,为了确定小岛C的具体位置,现在以A点为坐标原点,以正北方向为y轴正方向,以正东方向为x轴正方向建立平面直角坐标系(如图所示).请你帮助计算小岛所在位置的坐标(在直角三角形中,30°角所对的直角边为斜边的一半).
一轮船正向东以30海里/小时的速度航行,在A点处发现北偏东60°的方向有一小岛C,又航行2小时后,发现小岛C在北偏东30°方向,为了确定小岛C的具体位置,现在以A点为坐标原点,以正北方向为y轴正方向,以正东方向为x轴正方向建立平面直角坐标系(如图所示).请你帮助计算小岛所在位置的坐标(在直角三角形中,30°角所对的直角边为斜边的一半).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com