
| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 50 | 40 | 30 | 20 | 10 | … |
分析 (1)观察表格中的数据猜想y与x为一次函数关系,利用待定系数法求出k与b的值,确定出一次函数解析式,检验即可;
(2)设工艺品商店试销该工艺品每天获得的利润是W元,根据利润=销售总价-成本总价列出W与x的关系式,利用二次函数性质求出W取最大时x的值即可;
(3)由(2)的结论及这种工艺品的销售单价不能超过38元,求出使每天销售该工艺品获得的利润最大时单价,以及最大利润.
解答 解:(1)根据表格中y与x之间的对应关系可猜想y与x是一次函数关系,
设这个一次函数为y=kx+b(k≠0),则有$\left\{\begin{array}{l}50=20k+b\\ 40=30k+b.\end{array}\right.$
解得:$\left\{\begin{array}{l}k=-1\\ b=70.\end{array}\right.$,
∴y=-x+70,
将其余各点(40,30),(50,20),(60,10)代入y=-x+70中,均满足,
则所求的函数表达式为y=-x+70;
(2)设工艺品商店试销该工艺品每天获得的利润是W元,
依题意,得W=(x-10)(-x+70)=-x2+80x-700=-(x-40)2+900,
∴当x=40时,W有最大值,
则当销售单价定为40元时,商店试销该工艺品每天获得的利润最大;
(3)对于函数W=-(x-40)2+900,当x≤38时,W的值随着x值的增大而增大,
∴销售单价定为38元∕件时,工艺品商店试销该工艺品每天获得的利润最大,最大利润为W=-(38-40)2+900=896(元),
则当销售单价定为38元时,商店销售该工艺品每天可获得896元的最大利润.
点评 此题考查了二次函数的应用,涉及的知识有:待定系数法求一次函数解析式,二次函数的性质,熟练掌握二次函数性质是解本题的关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:填空题
 利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.
利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.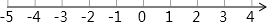
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
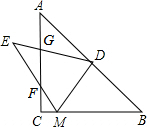 如图,已知点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.若△FCM的周长为16,则斜边AB的长为( )
如图,已知点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.若△FCM的周长为16,则斜边AB的长为( )| A. | 4$\sqrt{2}$ | B. | 8$\sqrt{2}$ | C. | 16$\sqrt{2}$ | D. | 32$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.
某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
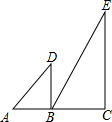 如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )
如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )| A. | 90° | B. | 45° | C. | 45°或90° | D. | 45°或90°或135° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com