
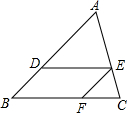
 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 由DE∥BC可得出∠ADE=∠B,结合∠ADE=∠EFC可得出∠B=∠EFC,进而可得出BD∥EF,结合DE∥BC可证出四边形BDEF为平行四边形,根据平行四边形的性质可得出DE=BF,由DE∥BC可得出△ADE∽△ABC,根据相似三角形的性质可得出BC=$\frac{8}{5}$DE,再根据CF=BC-BF=$\frac{3}{5}$DE=6,即可求出DE的长度.
解答 解:∵DE∥BC,
∴∠ADE=∠B.
∵∠ADE=∠EFC,
∴∠B=∠EFC,
∴BD∥EF,
∵DE∥BF,
∴四边形BDEF为平行四边形,
∴DE=BF.
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$=$\frac{AD}{AD+BD}$=$\frac{5}{8}$,
∴BC=$\frac{8}{5}$DE,
∴CF=BC-BF=$\frac{3}{5}$DE=6,
∴DE=10.
故选C.
点评 本题考查了相似三角形的判定与性质、平行线的性质以及平行四边形的判定与性质,根据相似三角形的性质找出BC=$\frac{8}{5}$DE是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{54}$ | B. | $\frac{13}{54}$ | C. | $\frac{1}{13}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
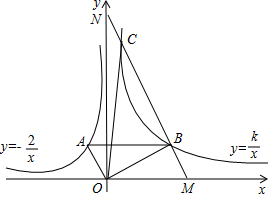 如图,∠AOB=90°,反比例函数y=-$\frac{2}{x}$(x<0)的图象过点A(-1,a),反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象过点B,且AB∥x轴.
如图,∠AOB=90°,反比例函数y=-$\frac{2}{x}$(x<0)的图象过点A(-1,a),反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象过点B,且AB∥x轴.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
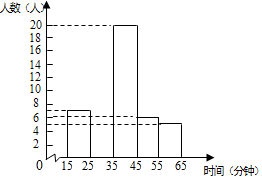 某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.| 组别 | 分组 | 频数 | 频率 |
| 1 | 15~25 | 7 | 0.14 |
| 2 | 25~35 | a | 0.24 |
| 3 | 35~45 | 20 | 0.40 |
| 4 | 45~55 | 6 | b |
| 5 | 55~65 | 5 | 0.10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com