
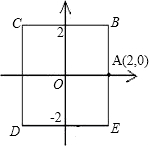
 如图,物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以l单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2011次相遇地点的坐标是________.
如图,物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以l单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2011次相遇地点的坐标是________.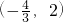
 =
= ,物质B行的路程为16×
,物质B行的路程为16×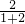 =
= ,在BC边相遇;
,在BC边相遇; =
= ,物质B行的路程为16×2×
,物质B行的路程为16×2×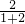 =
= ,在DE边相遇;
,在DE边相遇; =16,物质B行的路程为16×3×
=16,物质B行的路程为16×3×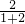 =32,相遇甲乙行的路程和为4a,甲行的路程为4a×
=32,相遇甲乙行的路程和为4a,甲行的路程为4a× =a,乙行的路程为4a×
=a,乙行的路程为4a×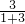 =3a,在A点相遇;
=3a,在A点相遇; =
= ,物质B行的路程为16×4×
,物质B行的路程为16×4×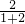 =
= ,在BC边相遇;
,在BC边相遇; =
=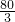 ,物质B行的路程为16×5×
,物质B行的路程为16×5×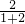 =
= ,在DE边相遇;
,在DE边相遇; -2)=-
-2)=- ,所以它们第2011次相遇在边BC上,点的坐标是
,所以它们第2011次相遇在边BC上,点的坐标是 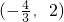 .
.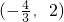 .
.

科目:初中数学 来源: 题型:
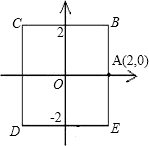 如图,物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以l单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2011次相遇地点的坐标是
如图,物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以l单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2011次相遇地点的坐标是查看答案和解析>>
科目:初中数学 来源:2010年浙江省温州市瓯海中学高一实验班选拔考试数学试卷(解析版) 题型:填空题
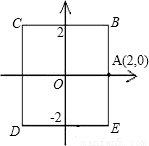 如图,物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以l单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2011次相遇地点的坐标是 .
如图,物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以l单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2011次相遇地点的坐标是 .查看答案和解析>>
科目:初中数学 来源:2008年湖南省长沙市长郡中学高一自主招生数学试卷(解析版) 题型:填空题
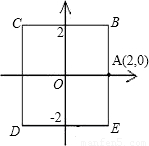 如图,物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以l单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2011次相遇地点的坐标是 .
如图,物质A与物质B分别由点A(2,0)同时出发,沿正方形BCDE的周界做环绕运动,物质A按逆时针方向以l单位/秒等速运动,物质B按顺时针方向,以2单位/秒等速运动,则两个物质运动后的第2011次相遇地点的坐标是 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com