
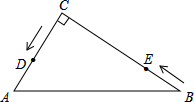
 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C→A→B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为ts(0<t<8).
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C→A→B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为ts(0<t<8).分析 (1)直接利用勾股定理和三角函数计算;
(2)当△BDE是直角三角形时,∠B不可能为直角,所以分两种情况讨论:i)图1,当∠BED=90°时;ii)图2,当∠EDB=90°时;利用相似求边,再利用同角三角函数值列等式计算求出t的值;
(3)①根据点D的位置分两种情况讨论:点D在边AC上时,0<t≤3;点D在边AB上时,3<t<8;?CDEF的面积都等于△CDE面积的二倍;
②当?CDEF为菱形,对角线CE和DF互相垂直且平分,利用BH=BE+EH列式计算.
解答 解:(1)由勾股定理得:AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
sinB=$\frac{AC}{AB}=\frac{6}{10}$=$\frac{3}{5}$,
故答案为:10,$\frac{3}{5}$;
(2)如图1,当∠BED=90°时,△BDE是直角三角形,
则BE=t,AC+AD=2t ,
,
∴BD=6+10-2t=16-2t,
∵∠BED=∠C=90°,
∴DE∥AC,
∴$\frac{BE}{BC}=\frac{DE}{AC}$,
∴$\frac{t}{8}=\frac{DE}{6}$,
∴DE=$\frac{3t}{4}$,
∵sinB=$\frac{DE}{BD}$=$\frac{3}{5}$,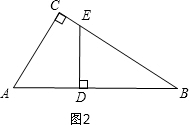
∴$\frac{\frac{3t}{4}}{16-2t}$=$\frac{3}{5}$,
t=$\frac{64}{13}$;
如图2,当∠EDB=90°时,△BDE是直角三角形,
则BE=t,BD=16-2t,
cosB=$\frac{BD}{BE}=\frac{BC}{AB}$=$\frac{8}{10}$,
∴$\frac{16-2t}{t}$=$\frac{8}{10}$,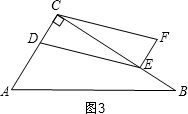
∴t=$\frac{40}{7}$;
答:当△BDE是直角三角形时,t的值为$\frac{64}{13}$或$\frac{40}{7}$;
(3)①如图3,当0<t≤3时,BE=t,CD=2t,CE=8-t,
∴S?CDEF=2S△CDE=2×$\frac{1}{2}$×2t×(8-t)=-2t2+16t,
如图4,当3<t<8时,BE=t,CE=8-t,
过D作DH⊥BC,垂足为H,
∴DH∥AC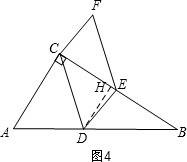 ,
,
∴$\frac{DH}{AC}=\frac{BD}{AB}$,
∴$\frac{DH}{6}=\frac{16-2t}{10}$,
∴DH=$\frac{3(16-2t)}{5}$,
∴S?CDEF=2S△CDE=2×$\frac{1}{2}$×CE×DH=CE×DH=(8-t)•$\frac{3(16-2t)}{5}$=$\frac{6}{5}{t}^{2}-\frac{96}{5}t+\frac{384}{5}$;
∴S于t的函数关系式为:当0<t≤3时,S=-2t2+16t,
当3<t<8时,S=$\frac{6}{5}{t}^{2}-\frac{96}{5}t+\frac{384}{5}$;
②存在,如图5,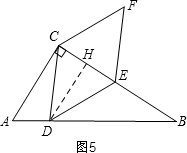 当?CDEF为菱形时,DH⊥CE,
当?CDEF为菱形时,DH⊥CE,
由CD=DE得:CH=HE,
BH=$\frac{4(16-2t)}{5}$,BE=t,EH=$\frac{8-t}{2}$,
∴BH=BE+EH,
∴$\frac{4(16-2t)}{5}$=t+$\frac{8-t}{2}$,
∴t=$\frac{88}{21}$,
即当t=$\frac{88}{21}$时,?CDEF为菱形.
点评 本题是四边形和三角形的综合问题,以两个动点为背景,考查了平行四边形、菱形、直角三角形的性质,考查了利用平行线分线段成比例定理求边长或表示边长;难度适中,是一个不错的四边形的综合题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 2,$\sqrt{2}$,4 | B. | 4,5,6 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a$≤\frac{17}{2}$ | B. | a≤12 | C. | a<$\frac{17}{2}$ | D. | a<12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
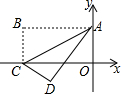 如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )| A. | (-$\frac{12}{5}$,-$\frac{6}{5}$) | B. | (-$\frac{12}{5}$,-$\frac{8}{5}$) | C. | ($\frac{12}{5}$,-$\frac{6}{5}$) | D. | ($\frac{12}{5}$,-$\frac{8}{5}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
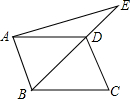 如图,点E在平行四边形ABCD的对角线BD的延长线上.
如图,点E在平行四边形ABCD的对角线BD的延长线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com