已知x+4y+z=24，2x+7y+2z=41，求x+y+z的值．
解：由已知得
设x+y+z=m（x+4y+z）+n（2x+7y+2z）=（m+2n）x+（4m+7n）y+（m+2n）z
比较系数，得
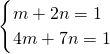
，解得
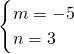
∴x+y+z=m（x+4y+z）+n（2x+7y+2z）=-5×24+3×41=3．
分析：此方程组是三元一次方程组，由于只有两个三元一次方程，因而要分别求出x、y、z的值是不可能的，但注意到所求的是x+y+z的代数和，因此，我们可通过设待定系数，解方程组得到．
点评：本题是三元不定方程组，解决这类问题，需要设待定系数，比较系数求解．本题也可以先求y，再求x+z，得出x+y+z的值．
浙大优学小学年级衔接捷径浙江大学出版社系列答案
