
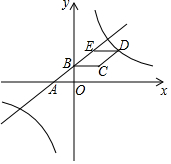
 ��ͼ����ƽ��ֱ������ϵ�У�����BCDE��һ��BCƽ����x�ᣬ��D�ڵ�һ���ޣ�ֱ��y=$\frac{3}{4}$x+3��x�ύ�ڵ�A����y�ύ�ڵ�B����������E���ҵ�B��AE���е㣬��D�ڷ���������y=$\frac{k}{x}$��k��0����ͼ���ϣ�
��ͼ����ƽ��ֱ������ϵ�У�����BCDE��һ��BCƽ����x�ᣬ��D�ڵ�һ���ޣ�ֱ��y=$\frac{3}{4}$x+3��x�ύ�ڵ�A����y�ύ�ڵ�B����������E���ҵ�B��AE���е㣬��D�ڷ���������y=$\frac{k}{x}$��k��0����ͼ���ϣ����� ��1��ͨ��һ�κ�������ʽ��B��0��3����A��-4��0���������õ�A���E���ڵ�B���ĶԳƵõ�E��4��6��������������ľ��빫ʽ�����BE=5��Ȼ��������ε����ʵõ���DE=BE=5��BC��DE��Ȼ��д��D�����ꣻ
��2����ȷ����������������ʽΪy=$\frac{54}{x}$���ټ������ε�����õ���FBC���������30����F��x��y�������ۣ�����F�ڵ�һ����ʱ�����������������ʽ�õ�$\frac{1}{2}$•5•��y-3��=30�����y=15��������Ӧ�ķ���������ֵ�õ���ʱF������ꣻ����F�ڵ�������ʱ������ͬ�������õ�F������ꣻ
��3����P��t��$\frac{3}{4}$t+3��������ƽ���ı��ε����ʵ�PQ��BC��PQ=BC=5����Q��t-5��$\frac{3}{4}$t+3����t+5��$\frac{3}{4}$t+3�������ۣ���Q������Ϊ��t-5��$\frac{3}{4}$t+3�������÷���������ͼ���ϵ�����������õ���t-5��•��$\frac{3}{4}$t+3��=54����Q������Ϊ��t+5��$\frac{3}{4}$t+3����ͬ���õ���t+5��•��$\frac{3}{4}$t+3��=54��Ȼ��ֱ�ⷽ�����t��ֵ���Ӷ��õ�����������Q��ĺ����꣮
��� �⣺��1����x=0ʱ��y=$\frac{3}{4}$x+3=3����B��0��3����
��y=0ʱ��$\frac{3}{4}$x+3=0�����x=-4����A��-4��0����
�ߵ�B��AE���е㣬
���A���E���ڵ�B���ĶԳƣ�
��E��4��6����
��BE=$\sqrt{{4}^{2}+��6-3��^{2}}$=5��
���ı���BCDEΪ���Σ�
��DE=BE=5��BC��DE��
��BCƽ����x�ᣬ
��DE��x�ᣬ
��D��9��6����
��2����D��9��6������y=$\frac{k}{x}$��k=9��6=54��
�෴������������ʽΪy=$\frac{54}{x}$��
������BCDE�����=5��3=15��
�ߡ�FBC�������������BCDE�����2����
���FBC���������30��
��F��x��y����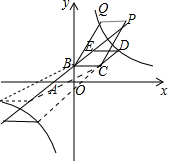
����F�ڵ�һ����ʱ��
��$\frac{1}{2}$•5•��y-3��=30�����y=15��
��y=15ʱ��$\frac{54}{x}$=15�����x=$\frac{18}{5}$����ʱF�������Ϊ��$\frac{18}{5}$��15����
����F�ڵ�������ʱ��
��$\frac{1}{2}$•5•��3-y��=30�����y=-9��
��y=-9ʱ��$\frac{54}{x}$=-9�����x=-6����ʱF�������Ϊ��-6��-9����
������������F��������$\frac{18}{5}$��15����-6��-9����
��3����P��t��$\frac{3}{4}$t+3����
��B��C��P��QΪ������ı�����ƽ���ı��Σ�
��PQ��BC��PQ=BC=5��
��Q��t-5��$\frac{3}{4}$t+3����t+5��$\frac{3}{4}$t+3����
��Q��������t-5��$\frac{3}{4}$t+3����
��Q��t-5��$\frac{3}{4}$t+3������y=$\frac{54}{x}$�ã�t-5��•��$\frac{3}{4}$t+3��=54��
������t2-t-92=0�����t1=$\frac{1+\sqrt{329}}{2}$��t2=$\frac{1-\sqrt{329}}{2}$��
��ʱQ��ĺ�����Ϊ$\frac{-9+\sqrt{329}}{2}$��$\frac{-9-\sqrt{329}}{2}$��
��Q��������t+5��$\frac{3}{4}$t+3����
��Q��t+5��$\frac{3}{4}$t+3������y=$\frac{54}{x}$�ã�t+5��•��$\frac{3}{4}$t+3��=54��
������t2+4t-52=0�����t1=4����ȥ����t2=-13��
��ʱQ��ĺ�����Ϊ-8��
������������Q�ĺ�����Ϊ$\frac{-9+\sqrt{329}}{2}$��$\frac{-9-\sqrt{329}}{2}$��-8��
���� ���⿼���˷������������ۺ��⣺�������շ���������ͼ���ϵ���������������ε����ʺ�ƽ���ı��ε����ʣ�����һ�κ���������Ľ�������ͽ�һԪ���η��̣�����������ͼ�����ʣ���ס�����ľ��빫ʽ�������÷������۵�˼������ѧ���⣮


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��107�� | B�� | 2��108�� | C�� | 2��10-7�� | D�� | 2��10-8�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
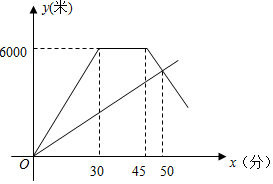 �����������6000�ף��������ΰͬʱ�Ӽس�������ǰ���ҵأ���������ҵغ���Ϣһ��ʱ�����ԭ�����ٶȴ�ԭ·���أ���ͼ��ʾ��������صľ���y���ף������ʱ��x���֣�֮��ĺ���ͼ��
�����������6000�ף��������ΰͬʱ�Ӽس�������ǰ���ҵأ���������ҵغ���Ϣһ��ʱ�����ԭ�����ٶȴ�ԭ·���أ���ͼ��ʾ��������صľ���y���ף������ʱ��x���֣�֮��ĺ���ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
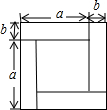 ��ͼ������ȫ��ͬ���ĸ�������ֽƬƴ��һ����������Σ������ֲ�ͬ�ķ�����ʾ����������ε����������Եó�һ����ʽΪ��������
��ͼ������ȫ��ͬ���ĸ�������ֽƬƴ��һ����������Σ������ֲ�ͬ�ķ�����ʾ����������ε����������Եó�һ����ʽΪ��������| A�� | ��a+b��2=a2+2ab+b2 | B�� | ��a-b��2=a2-2ab+b2 | C�� | a2-b2=��a+b����a-b�� | D�� | ��a+b��2=��a-b��2+4ab |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ���� | C�� | �ཻ | D�� | ���ж� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
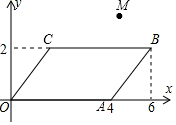 ��ͼ����ƽ��ֱ������ϵxOy�У��ı���OABC��ƽ���ı��Σ���A��4��0����B��6��2����M��4��3������ƽ������һ������M��ֱ�߽�ƽ���ı���OABC������ֳ���ȵ������֣���д����ֱ�ߵĺ�������ʽy=2x-5��
��ͼ����ƽ��ֱ������ϵxOy�У��ı���OABC��ƽ���ı��Σ���A��4��0����B��6��2����M��4��3������ƽ������һ������M��ֱ�߽�ƽ���ı���OABC������ֳ���ȵ������֣���д����ֱ�ߵĺ�������ʽy=2x-5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��y-1��2=$\frac{3}{2}$ | B�� | ��y+1��2=$\frac{3}{2}$ | C�� | ��y+$\frac{1}{2}$��2=$\frac{3}{4}$ | D�� | ��y-$\frac{1}{2}$��2=$\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������y=2x��y=ax+4��ͼ���ཻ�ڵ�A��$\frac{3}{2}$��3������ʽ2x��ac+4�Ľ⼯Ϊ��������
��ͼ������y=2x��y=ax+4��ͼ���ཻ�ڵ�A��$\frac{3}{2}$��3������ʽ2x��ac+4�Ľ⼯Ϊ��������| A�� | x��$\frac{3}{2}$ | B�� | x��3 | C�� | x��$\frac{3}{2}$ | D�� | x��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x2+18x+84 | B�� | y=x2+2x+4 | C�� | y=x2+18x+76 | D�� | y=x2+2x-2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com