
分析 先将(x+1-$\frac{3}{x-1}$)×$\frac{x-1}{x-2}$进行化简,然后将x=-$\frac{2}{\sqrt{2}+2}$代入求解即可.
解答 解:$({x+1-\frac{3}{x-1}})•\frac{x-1}{x-2}$
=$[\frac{(x+1)(x-1)}{x-1}-\frac{3}{x-1}]×\frac{x-1}{x-2}$
=$\frac{{{x^2}-4}}{x-1}×\frac{x-1}{x-2}$
=$\frac{(x+2)(x-2)}{x-2}$
=x+2.
当$x=-\frac{2}{{\sqrt{2}+2}}$=$-\frac{{2(\sqrt{2}-2)}}{{(\sqrt{2}+2)(\sqrt{2}-2)}}=\sqrt{2}-2$时,
原式=$\sqrt{2}-2+2$=$\sqrt{2}$.
点评 本题考查了分式的化简求值,解答本题的关键在于先将(x+1-$\frac{3}{x-1}$)×$\frac{x-1}{x-2}$进行化简,然后将x=-$\frac{2}{\sqrt{2}+2}$代入求解.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
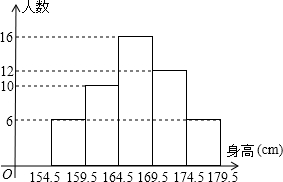 为了了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得打的数据(身高取整数)整理后,画出频数分布直方图(如图所示),图中从左到右依次为第1,2,3,4,5组.
为了了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得打的数据(身高取整数)整理后,画出频数分布直方图(如图所示),图中从左到右依次为第1,2,3,4,5组.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔40海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.问B处距离灯塔P有多远?(结果精确到0.1海里)
如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔40海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.问B处距离灯塔P有多远?(结果精确到0.1海里)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
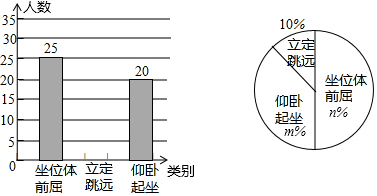
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com