
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 把x=-2代入y=ax2+bx+c得:y=4a-2b+c=0即可判断①;求出a b c的符号,根据两个根之和为负且-$\frac{b}{a}$>-1,即可判断⑤,根据4a-2b+c=0和a+b+c>0即可判断④,根据-1<-$\frac{b}{2a}$<0,求出后即可判断②,根据4a-2b+c=0推出2a-b=-$\frac{1}{2}$c,根据二次函数与y轴的交点位置即可判断③.
解答 解:∵二次函数的图象与x轴交于点(-2,0)、(x1,0),且1<x1<2,
∴把x=-2代入y=ax2+bx+c得:y=4a-2b+c=0,∴①正确;
∵二次函数的图象开口向下,
∴a<0,
∵二次函数的图象与x轴交于点(-2,0)、(x1,0),且1<x1<2,
∴两根之积为负,$\frac{c}{a}$<0,即c>0,
-$\frac{b}{2a}$<0,即a、b同号,b<0,
两个根之和为负且-$\frac{b}{a}$>-1,即a<b<0,∴⑤正确;
∵把(-2,0)代入y=ax2+bx+c得:4a-2b+c=0,
∴即2b=4a+c<0(因为b<0),
∵当x=1时,a+b+c>0,
∴2a+2b+2c>0,
∴6a+3c>0,
即2a+c>0,∴④错误;
∵二次函数的图象与x轴交于点(-2,0)、(x1,0),且1<x1<2,
∴-1<-$\frac{b}{2a}$<0,
∵a<0,
∴-2a>-b,
∴0>2a-b,
即2a-b<0,∴②正确;
∵把x=-2代入y=ax2+bx+c得:y=4a-2b+c=0,
4a-2b=-c,
2a-b=-$\frac{1}{2}$c,
∵O<c<2,
∴2a-b>-1,
∴③正确;
正确的有4个.
故选C.
点评 本题考查了二次函数图象与系数的关系,主要考查学生根据图形进行推理和辨析的能力,用了数形结合思想,题目比较好,但是难度偏大.


科目:初中数学 来源:2017届山东省济南市天桥区九年级学业水平考试第一次模拟数学试卷(解析版) 题型:单选题
下列图形中,既是轴对称图形又是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$,2,$\sqrt{5}$ | B. | 3,4,6 | C. | 1,$\sqrt{3}$,2 | D. | 6,8,12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
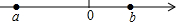 如图:a,b是数轴上的两点,化简$\sqrt{{a^2}-2ab+{b^2}}$+$\sqrt{{a^2}+2ab+{b^2}}$=-2a.
如图:a,b是数轴上的两点,化简$\sqrt{{a^2}-2ab+{b^2}}$+$\sqrt{{a^2}+2ab+{b^2}}$=-2a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
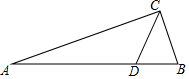 如图所示,在Rt△ABC中,斜边AB=3,BC=1,点D在AB上,且$\frac{BD}{AD}$=$\frac{1}{3}$,则tan∠BCD的值是( )
如图所示,在Rt△ABC中,斜边AB=3,BC=1,点D在AB上,且$\frac{BD}{AD}$=$\frac{1}{3}$,则tan∠BCD的值是( )| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com