
 米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为圆点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0)
米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为圆点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0)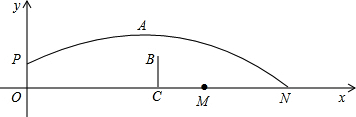
 )代入可得:
)代入可得: =a(0-5)2+3,
=a(0-5)2+3, ,
, (x-5)2+3.
(x-5)2+3. (x-5)2+3=0,
(x-5)2+3=0, (舍去),x2=5+3
(舍去),x2=5+3 ,
, ,
, -1(米).
-1(米). (m-5)2+3=2.4,
(m-5)2+3=2.4, )代入可得出a的值,继而得出抛物线解析式;
)代入可得出a的值,继而得出抛物线解析式;

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com