B
分析:分三种情况讨论a的取值范围:①a=3,②a>3,③a<3,再去绝对值符号进行求解.
解答:原方程为|3x|=ax+1.
①若a=3,则|3x|=3x+1.
当x<0时,-3x=3x+1,∴x=-

;
当x≥0时,3x=3x+1,不成立;
∴当a=3时,原方程的根为:x=-

;
②若a>3,当x<0时,-3x=ax+1,∴x=

<0;
当x≥0时,3x=ax+1,∴x=

<0,矛盾,
∴当a>3时,原方程的解为:x=

<0.
③若a<3时,当x≥0时,3x=ax+1,∴x=
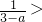
0,
∴原方程的根是正数,不符合题意.
综上所述:当a≥3时,原方程的根是负根.
故选B.
点评:本题考查了含绝对值符号的一元一次方程,难度较大,关键是分类讨论a的取值范围后再进行求解.

 ;
; ;
; <0;
<0; <0,矛盾,
<0,矛盾, <0.
<0.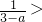 0,
0,
