Question

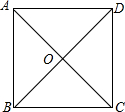
在四边形ABCD中，对角线AC、BD相交于点O，其中AC+BD=28，CD=10．
（1）若四边形ABCD是平行四边形，则△OCD的周长为________；
（2）若四边形ABCD是菱形，则菱形的面积为________；
（3）若四边形ABCD是矩形，则AD的长为________．

Answer 1

解：
（1）∵四边形ABCD是平行四边形，
∴OA=OC，OD=OB，
∵AC+BD=28，
∴OC+OD=14，
∴△OCD的周长为OD+OC+CD=24，
故答案为：24．

（2）∵OD+OC=14，CD=10，
∵四边形ABCD是菱形，
∴AC⊥BD，
由勾股定理得：OC²+OD²=CD²，
∴（0C+0D）²-2OC•OD=100，
∴OC×OD=48，
AC×BD=192，
∴菱形的面积为是AC×BD=96，
故答案为：96．

（3）∵矩形ABCD，
∴AC=BD=14，∠CDA=90°，
∵CD=10，
由勾股定理得：AD==4，
故答案为：4．
分析：（1）根据平行四边形性质求出OD+OC即可求出答案；
（2）根据矩形性质求出OD+OC，根据勾股定理求出OC×OD，进一步求出AC×BD，即可求出面积；
（3）根据矩形性质求出AC，根据勾股定理求出即可．
点评：本题主要考查对平行四边形性质，矩形性质，菱形性质，勾股定理等知识点的理解和掌握，能熟练地运用性质进行计算是解此题的关键．