阅读下面的作品,完成小题。
正则艺专
高尔泰
(1)宁沪线上位于镇江和无锡之间的丹阳市, 是一座毫无特色的小城;正则艺专所在的白云街,是一条毫无特色的小街,战后才从重庆迁回原址的。私立正则艺专,是几栋灰色的二层楼房,也毫无特色。但它拥有几位赫赫有名的教授,特别是吕凤子先生和杨守玉先生,吸引了许多来自全国各地的学生。
(2)吕凤子是学者型画家,精通理论,以画罗汉和菩萨著称,诗书印并重,是当时画坛的重镇。他所创办的正则艺专,论画极重意境,崇尚“文人画”传统的功力和品味成为名校,不是偶然的。我去时,他已很老,不再亲自上课,只当名义上的校长。穿着老式长衫,有时到画室里转转,有时拄着拐杖,在荒凉的校园里散步,矮小,瘦削,微微有点佝偻,眼镜的黑色边框很粗,就像是粗墨线画的。
(3)杨守玉是个很老的老太婆,终生未婚,索居独处。她所创造的画种“乱针绣”,是用针线代替画笔和色彩,在布上作画无数不同色彩不同长短的丝线,不规则地相互横斜交叉错综重叠,近看一片混沌无序,远看人物风景生气洋溢光影迷离,画法有点像印象派的点彩,但要用点彩法临摹它根本不行。它的每一幅都是独特和不可重复的,无论是深巷里墙高落日的余晖,灯影暗处的裸女,雨中的树或者阳光下灼灼生辉的一团黄花,都像是不久就会消逝的东西,猛一看你感受到的不是肌肤而是肌肤的温暖与弹性,不是雨水而是雨水的清冷和馨香,不是花团而是花团的快乐的喧嚷。再细看,又都没了。这很难。杨氏门生虽多,仍难免感到寂寞,有句云,“急管繁弦听无声”。
(4)她惟一的传人吕去疾先生,是凤先生的长子,五十多岁, 笔名大吕,也确实是黄钟大吕,不但乱针绣青出于蓝,油画、雕塑、大泼墨无不绝倒。据说艺事尚专,博则难精,我想那是才小者言,才大者若韩愈稼轩达芬奇杜尚辈,都能兴寄无端,忽豆人寸马,忽千丈松,何羁于专? 先生教画,很少讲具体技法。看某生画,他会说色彩能发出声音,阴沉有阴沉的响亮,那些用灰不溜秋的哑巴颜色来处理蓝调子的人,成不了大画家。看某生画,他会说画画是一种快乐,过程就是目的,要能随时停下都是好画,那种画时没有快乐,直要到画完了才算苦尽甘来的画家,是平庸的画家。看某生画,他会说, 小青年怎么就结壳了?艺术的生命是变化,结了壳就完蛋了。我听之悚然,刻骨铭心。
(5)其他老师,也都各有千秋。程虚白先生讲构图学,爱用书法做比喻,要我们从字形结构的变化吸取灵感;黄涵秋先生教书法,讲的却是音乐,135和弦和246和弦,还有武术的招式和舞蹈的动作,说书法就是纸上舞蹈,和无声的音乐;张祖源先生讲美术史,说史家们忽略了源远流长的指头画,说着当场就展纸磨墨,画给我们看。那指甲画出的细线轻悠而富于弹性,手掌抹出的墨痕波诡云谲,确有笔不能到之处。这种不拘一格挥洒自如的学风,我在别处再没见过 。
(6)正则学制,分二年三年五年三种。我在五年制,叫做“绘绣科”,到四年级可选学油画国画雕刻,也可选学乱针绣。乱针绣是正则的王牌,绘绣科就是为它设立的,别的院校没有。但它太难,只有几个人选学,练就一套从画布正反两面同时反向穿刺的技巧,速度之快,就像两只手都在高频率颤抖,但是绣出来的作品,吕去疾先生说,只能算是工艺品。他们到头来,还是选学了别的,否则不得毕业。但我们班上的同学,都想走这畏途,想成为这门绝技的第二代传人,很用功。每个人画好的画,都要钉在墙上,互相观摩品评。画室墙上一排排新作,呈现出一股子欣荣进取的气氛。画室日夜不关,晚上十点以前,总有人在灯下作画。我那时十五岁,是全校年龄最小的一个,画名挺好,颇受注意,所以也不再撒野,变成了规矩学生。
【小题1】文章开头连续说丹阳、白云街和正则艺专建筑的“毫无特色”,为什么要这样写?从文章内容和表达效果两方面来说明。(4分)
【小题2】第三小节的划线句子是从哪几个角度来描写杨守玉的乱针绣内容的?写出了乱针绣怎样的特点?(4分)
【小题3】根据文章第四小节的内容,概括吕去疾先生的艺术成就和艺术观。(6分)
【小题4】结合全文内容,从教师和学生这两方面总结正则艺专取得成功的原因。(6分)

 ”用代数式可以表示为
”用代数式可以表示为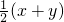
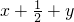
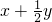
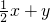
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案