解:(1)∵四边形ABCD是平行四边形,
∴AC=2OA,BD=2OB,
∵△AOB的周长为12,AB=5,
∴OA+OB+AB=12,
∴OA+OB=7,
∴AC+BD=2(OA+OB)=14;
(2)不能求出AC与BD分别是多少,
因为平行四边形的AC和BD只有互相平分,没有其它条件;
(3)设AO=x,则OB=7-x,
∵四边形ABCD是菱形,
∴AC⊥BD,
在Rt△AOB中,AB2=AO2+OB2,
52=x2+(7-x)2,
x1=3,x2=4,
当x=3时,7-x=4,AC=6,BD=8;
当x=4时,7-x=3,AC=8,BD=6;
答:AC和BD的长分别为6、8或8、6.
分析:(1)根据平行四边形性质得出AC=2OA,BD=2OB,求出AO+OB,即可求出答案;
(2)根据平行四边形的性质之一-平行四边形的对角线互相平分,即可得出答案;
(3)设AO=x,则OB=7-x,根据菱形的性质得出AC⊥BD,在Rt△AOB中,根据勾股定理得出52=x2+(7-x)2,求出即可.
点评:本题考查了平行四边形性质,菱形性质,勾股定理等知识点,用了方程思想.

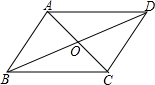 在?ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为12,AB=5,
在?ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为12,AB=5,
