
 ,则线段EH的长为________.
,则线段EH的长为________. 或
或
 ;其次,在Rt△AEF中,利用勾股定理求出BE或DF的长度;然后在Rt△DFK中解直角三角形求出DK的长度,从而得到CK的长度,由AB∥CD,列比例式求出AH的长度;最后作HN∥AE,列出比例式求出EH的长度.
;其次,在Rt△AEF中,利用勾股定理求出BE或DF的长度;然后在Rt△DFK中解直角三角形求出DK的长度,从而得到CK的长度,由AB∥CD,列比例式求出AH的长度;最后作HN∥AE,列出比例式求出EH的长度.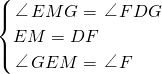
 .(直角三角形斜边上的中线长等于斜边长的一半)
.(直角三角形斜边上的中线长等于斜边长的一半)
 )2,
)2, .
. ,
, .
.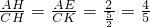 ,
, ,∴AH=
,∴AH= AC=
AC= .
. AH=
AH= .
. ,即
,即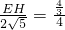 ,
, ;
;
 .
. 或
或 .
. 或
或 .
.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
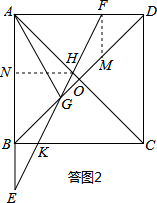
 (2013•临沂)如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
(2013•临沂)如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com