
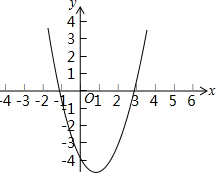
 设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{-1,-1}=-1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:
设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{-1,-1}=-1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:分析 (1)根据max{a,b}表示a、b两数中较大者,即可求出结论;
(2)根据max{3x+1,-x+1}=-x+1,即可得出关于x的一元一次不等式,解之即可得出结论;
(3)联立两函数解析式成方程组,解之即可求出交点坐标,画出直线y=-x+2的图象,观察图形,即可得出max{-x+2,x2-2x-4}的最小值.
解答 解:(1)max{5,2}=5,max{0,3}=3.
故答案为:5;3.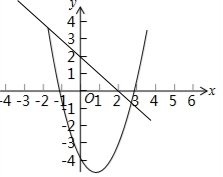
(2)∵max{3x+1,-x+1}=-x+1,
∴3x+1≤-x+1,
解得:x≤0.
(3)联立两函数解析式成方程组,
$\left\{\begin{array}{l}{y={x}^{2}-2x-4}\\{y=-x+2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=-1}\end{array}\right.$,
∴交点坐标为(-2,4)和(3,-1).
画出直线y=-x+2,如图所示,
观察函数图象可知:当x=3时,max{-x+2,x2-2x-4}取最小值-1.
点评 本题考查了二次函数的最值、一次函数的图象、一次函数的性质以及二次函数的图象,解题的关键是:(1)读懂题意,弄清max的意思;(2)根据max{3x+1,-x+1}=-x+1,找出关于x的一元一次不等式;(3)联立两函数解析式成方程组,通过解方程组求出交点坐标.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
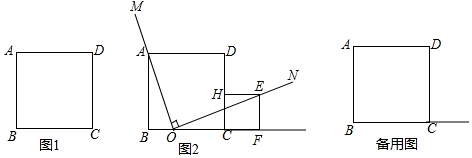
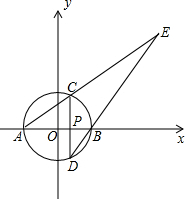 如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.
如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
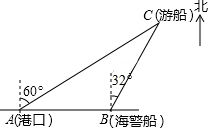 (7分)一艘游船从港口A处以北偏东60°的方向出港观光.航行170海里至C处时发生了事故.船长立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东32°方向.若海警船以60海里/时的速度前往救援,求海警船到达事故船C处大约所需的时间.(精确到0.1小时)【参考数据:sin32°=0.53,cos32°=0.85.tan32°=0.62】
(7分)一艘游船从港口A处以北偏东60°的方向出港观光.航行170海里至C处时发生了事故.船长立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东32°方向.若海警船以60海里/时的速度前往救援,求海警船到达事故船C处大约所需的时间.(精确到0.1小时)【参考数据:sin32°=0.53,cos32°=0.85.tan32°=0.62】查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
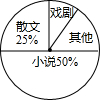 八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.| 类别 | 频数(人数) | 频率 |
| 小说 | 0.5 | |
| 戏剧 | 4 | |
| 散文 | 10 | 0.25 |
| 其他 | 6 | |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3<x≤2 | B. | -3≤x<2 | C. | x≥2 | D. | x<-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com